①②④
分析:根据含有量词的命题的否定,可得①是真命题;根据幂函数的定义、图象和性质,得②是真命题;通过举出反例说明,得到③是假命题;根据正切函数的单调性和函数图象的变换,可得④是真命题;根据指、对数函数的单调性和充分必要条件的含义,得到⑤是假命题.
解答:对于①,命题“?x∈R,使2
x≤3”是一个全称性命题,
它的否定应该是改量词为“存在”,再否定结论,得①是真命题;
对于②,若函数f(x)=(m
2-m-1)x
m是幂函数,则m
2-m-1=1,解之得m=2或-1
∴幂函数为f(x)=x
2或f(x)=x
-1,
结合函数f(x)在x∈(0,+∞)上是增函数,得m是正数,只有m=2符合,故②是真命题;
对于③,命题“函数f(x)在x=x
0处有极值,则f
′(x
0)=0”的否命题是
“函数f(x)在x=x
0处没有极值,则f
′(x
0)≠0”,
以函数y=x
3为例,它在x=0处没有极值,但f
′(x
0)=0仍然成立,故③是假命题;
对于④,令-

+kπ<

<

+kπ,k∈Z.得-

+kπ<x<

+kπ,k∈Z.
取k=0,得区间(-

,

),刚好包含区间
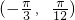
,
因此,函数
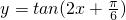
在区间
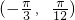
上单调递增;
对于⑤,由“log
2x>log
3x”,可得x>1,得不出“2
x>3
x”成立,
反之,当“2
x>3
x”成立,可得x<0,显然“log
2x>log
3x”不成立
“log
2x>log
3x”是“2
x>3
x”的既不充分也不必要条件,故⑤是假命题.
故答案为:①②④
点评:本题以命题真假的判断为载体,考查了含有量词的命题否定、函数的极值与单调性、三角函数的图象与性质和指对数函数的图象与性质等知识,属于基础题.

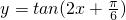 在区间
在区间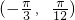 上单调递增;
上单调递增; +kπ<
+kπ< <
< +kπ,k∈Z.得-
+kπ,k∈Z.得- +kπ<x<
+kπ<x< +kπ,k∈Z.
+kπ,k∈Z. ,
, ),刚好包含区间
),刚好包含区间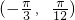 ,
,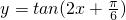 在区间
在区间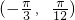 上单调递增;
上单调递增;

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案