
【题目】已知二次函数y=f(x)最大值为3,且f(﹣4)=f(0)=﹣1
(1)求f(x)的解析式;
(2)求f(x)在[﹣3,3]上的最值.
【答案】
(1)解:因为f(﹣4)=f(0),
所以二次函数的对称轴为:x=﹣2,
又y=f(x)的最大值为3,
所以可设二次函数为f(x)=a(x+2)2+3,
因为f(0)=﹣1,所以a(0+2)2+3=﹣1,解得a=﹣1,
所以f(x)=﹣(x+2)2+3
(2)解:因为﹣2∈[﹣3,3],
所以f(x)max=f(﹣2)=3,
当x=3时,f(x)min=f(3)=﹣22
【解析】(1)由f(﹣4)=f(0)可得对称轴x=﹣2,再由最大值为3可设f(x)=a(x+2)2+3,根据f(0)=﹣1即可求得a值;(2)结合二次函数的图象特征即可求得其最值;
【考点精析】本题主要考查了二次函数在闭区间上的最值的相关知识点,需要掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 才能正确解答此题.
才能正确解答此题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ) 求曲线![]() 与
与![]() 交点的平面直角坐标;
交点的平面直角坐标;
(Ⅱ) 点![]() 分别在曲线
分别在曲线![]() ,
, ![]() 上,当
上,当![]() 最大时,求
最大时,求![]() 的面积(
的面积(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且f(1)=2,f(2)=3. (I)若f(x)是偶函数,求出f(x)的解析式;
,且f(1)=2,f(2)=3. (I)若f(x)是偶函数,求出f(x)的解析式;
(II)若f(x)是奇函数,求出f(x)的解析式;
(III)在(II)的条件下,证明f(x)在区间 ![]() 上单调递减.
上单调递减.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 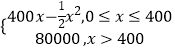 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.
(1)在图中画出过点![]() 的平面
的平面![]() ,使得
,使得![]() 平面
平面![]() (必须说明画法,不需证明);
(必须说明画法,不需证明);
(2)若二面角![]() 是
是![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次函数f(x)是R上的增函数,已知f[f(x)]=16x+5,g(x)=f(x)(x+m).
(1)求f(x);
(2)若g(x)在(1,+∞)单调递增,求实数m的取值范围;
(3)当x∈[﹣1,3]时,g(x)有最大值13,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
比较关注 | 不太关注 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:![]() ,
,![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com