
【题目】已知函数f(x)=ax3﹣bx+2(a>0)
(1)在x=1时有极值0,试求函数f(x)的解析式;
(2)求f(x)在x=2处的切线方程.
【答案】
(1)解:函数f(x)=ax3﹣bx+2的导数为f′(x)=3ax2﹣b,
在x=1时有极值0,可得f(1)=0,且f′(1)=0,
即为a﹣b+2=0,且3a﹣b=0,
解得a=1,b=3,
可得f(x)=x3﹣3x+2
(2)解:f′(x)=3ax2﹣b,
可得f(x)在x=2处的切线斜率为12a﹣b,
切点为(2,8a﹣2b+2),
即有f(x)在x=2处的切线方程为y﹣(8a﹣2b+2)=(12a﹣b)(x﹣2),
化为(12a﹣b)x﹣y﹣16a+2=0
【解析】(1)求出f(x)的导数,可得f(1)=0,且f′(1)=0,得到a,b的方程,解方程可得a,b的值,进而得到f(x)的解析式;(2)求出f(x)的导数,可得切线的斜率和切点,由点斜式方程即可得到所求切线的方程.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() 且
且 ![]() ,
, ![]() 分别为
分别为 ![]() 的中点.
的中点.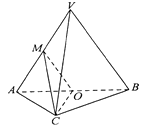
(1)求证: ![]() 平面
平面 ![]() .
.
(2)求证:平面 ![]() 平面
平面 ![]() .
.
(3)求三棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(0,+∞),3 ![]() +x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
+x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是 . ①
)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是 . ① ![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
② ![]() f(
f( ![]() )<f(
)<f( ![]() )
)
③f(0)>2f( ![]() )
)
④f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB= ![]() CD=1,M为PB的中点.
CD=1,M为PB的中点. 
(1)试在CD上确定一点N,使得MN∥平面PAD;
(2)点N在满足(1)的条件下,求直线MN与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 表示两条不同的直线,
表示两条不同的直线, ![]() 表示一个平面,给出下列四个命题:
表示一个平面,给出下列四个命题:
① ![]() ;②
;② ![]() ;
;
③ ![]() ;④
;④ ![]() .
.
其中正确命题的序号是( )
A.①②
B.②③
C.②④
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com