
【题目】![]() 年年初,新冠肺炎疫情防控工作全面有序展开.某社区对居民疫情防控知识进行了网上调研,调研成绩全部都在
年年初,新冠肺炎疫情防控工作全面有序展开.某社区对居民疫情防控知识进行了网上调研,调研成绩全部都在![]() 分到
分到![]() 分之间.现从中随机选取
分之间.现从中随机选取![]() 位居民的调研成绩进行统计,绘制了如图所示的频率分布直方图.
位居民的调研成绩进行统计,绘制了如图所示的频率分布直方图.
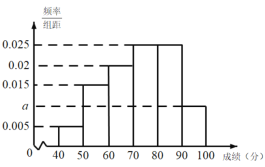
![]() 求
求![]() 的值,并估计这
的值,并估计这![]() 位居民调研成绩的中位数;
位居民调研成绩的中位数;
![]() 在成绩为
在成绩为![]() ,
,![]() 的两组居民中,用分层抽样的方法抽取
的两组居民中,用分层抽样的方法抽取![]() 位居民,再从
位居民,再从![]() 位居民中随机抽取
位居民中随机抽取![]() 位进行详谈.记
位进行详谈.记![]() 为
为![]() 位居民的调研成绩在
位居民的调研成绩在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列.
的分布列.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在原点
中心在原点![]() ,焦点在坐标轴上,直线
,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 另一个焦点是
另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与
与![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如表,其中一等奖代表队比三等奖代表队多10人.该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动.并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中二等奖代表队有5人(同队内男女生仍采用分层抽样)
名次 性别 | 一等奖 代表队 | 二等奖 代表队 | 三等奖 代表队 |
男生 | ? | 30 | ◎ |
女生 | 30 | 20 | 30 |
(1)从前排就坐的一等奖代表队中随机抽取3人上台领奖,用X表示女生上台领奖的人数,求X的分布列和数学期望E(X).
(2)抽奖活动中,代表队员通过操作按键,使电脑自动产生[﹣2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序.若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖.求代表队队员获得奖品的概率.
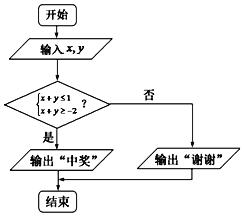
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
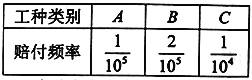
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com