分析:(1)连接A1D,则由A1D∥B1C?B1C与DE所成角即为A1D与DE所成角.在△A1ED中用余弦定理求解;
(2)取B1C的中点F,B1D的中点G,连接BF,EG,GF.由CD⊥平面BCC1B1?DC⊥BF?BF⊥平面B1CD,再由BF∥GE?GE⊥平面B1CD.?平面EB1D⊥B1CD;
(3)连接EF.CD⊥B1C,GF∥CD?GF⊥B1C?EF⊥B1C?∠EFG是二面角E-B1C-D的平面角,再在△EFG中求解.
解答: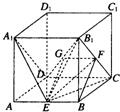
解:(1)连接A
1D,则由A
1D∥B
1C知,B
1C与DE所成角即为A
1D与DE所成角.连接A
1E,由正方体ABCD-A
1B
1C
1D
1,可设其棱长为a,则
A1D=a,A1E=DE=a∴
cos∠A1DE==∴直线B
1C与DE所成角的余弦值是
.(4分)
(2)取B
1C的中点F,B
1D的中点G,连接BF,EG,GF.
∵CD⊥平面BCC
1B
1,且BF?平面BCC
1B
1,
∴DC⊥BF.
又∵BF⊥B
1C,CD∩B
1C=C,
∴BF⊥平面B
1CD
又∵GF
CD,BE
CD,
∴GF
BE,
∴四边形BFGE是平行四边形,
∴BF∥GE,
∴GE⊥平面B
1CD.
∵CE?平面EB
1D,
∴平面EB
1D⊥B
1CD.(8分)
(3)连接EF.
∵CD⊥B
1C,GF∥CD,
∴GF⊥B
1C.
又∵GE⊥平面B
1CD,
∴EF⊥B
1C,
∴∠EFG是二面角E-B
1C-D的平面角.
设正方体的棱长为a,则在△EFG中,GF=
a,EF=
a,
∴
cos∠EFG==∴二面角E-B
1C-D的余弦值为
.(12分)
点评:本题主要通过异面直线所成的角和二面角来考查线线,线面,面面平行、垂直关系的转化.

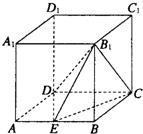 如图,已知正方体ABCD-A1B1C1D1中,E为AB的中点
如图,已知正方体ABCD-A1B1C1D1中,E为AB的中点 解:(1)连接A1D,则由A1D∥B1C知,B1C与DE所成角即为A1D与DE所成角.连接A1E,由正方体ABCD-A1B1C1D1,可设其棱长为a,则
解:(1)连接A1D,则由A1D∥B1C知,B1C与DE所成角即为A1D与DE所成角.连接A1E,由正方体ABCD-A1B1C1D1,可设其棱长为a,则

 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )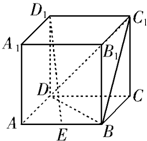 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.