
| A. | y=$\sqrt{x}$ | B. | y=|x|(x≥1) | C. | y=x${\;}^{\frac{2}{3}}$ | D. | y=x3+1 |
分析 先看函数的定义域是否关于原点对称,再看f(-x)与f(x)的关系,结合函数的奇偶性的定义,作出判断.
解答 解:由于y=$\sqrt{x}$的定义域为{x|x≥0},不关于原点对称,故该函数没有奇偶性,故排除A;
由于y=|x|(x≥1)的定义域不关于原点对称,故该函数没有奇偶性,故排除B;
由于y=${x}^{\frac{2}{3}}$=$\root{3}{{x}^{2}}$ 的定义域为R,且f(-x)=$\root{3}{{(-x)}^{2}}$=f(x),故该函数为偶函数,故C满足条件;
由于y=f(x)=x3+1,f(-x)=(-x)3+1=1-x3≠f(x),故该函数不是偶函数,
故选:C.
点评 本题主要考查函数的奇偶性的定义,判断函数的奇偶性的方法,属于基础题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{9}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | 1 | D. | $-\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
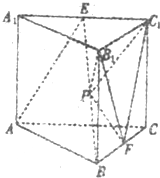 在直三棱柱ABC-A1B1C1 中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1 中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com