
【题目】据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2 ![]() ,(其中,t为关税的税率,且t∈[0,
,(其中,t为关税的税率,且t∈[0, ![]() ),x为市场价格,b,k为正常数),当t=
),x为市场价格,b,k为正常数),当t= ![]() 时的市场供应量曲线如图.
时的市场供应量曲线如图. 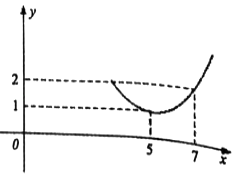
(Ⅰ)根据图象求b,k的值;
(Ⅱ)若市场需求量为Q(x)=2 ![]() ,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
.任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当t∈[﹣2,0]时,求函数g(t)的解析式;
(3)设函数h(x)=2|x﹣k|,H(x)=x|x﹣k|+2k﹣8,其中实数k为参数,且满足关于t的不等式 ![]() 有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD的中点. 
(1)求证:B1E⊥AD1
(2)若二面角A﹣B1E﹣A1的大小为30°,求AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在透明塑料制成的长方体ABCD﹣A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: ①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当E∈AA1时,AE+BF是定值.其中正确说法的是( )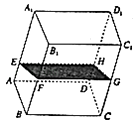
A.②③④
B.①②④
C.①③④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C的坐标分别为(﹣ ![]() ,0),(
,0),( ![]() ,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心. 
(1)写出重心G的坐标;
(2)求外心O′,垂心H的坐标;
(3)求证:G,H,O′三点共线,且满足|GH|=2|OG′|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=SB,点M是SD的中点,AN⊥SC,且交SC于点N. 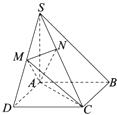
(1)求证:SC⊥平面AMN;
(2)求二面角D﹣AC﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把形如 ![]() 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得 ![]() ,两边对x求导数,得
,两边对x求导数,得 ![]() ,于是
,于是 ![]() ,运用此方法可以求得函数
,运用此方法可以求得函数 ![]() 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com