已知集合A={x|x2+x-6<0},集合B={x|3x2-5x-12≤0},求 CRA∩B,CRB∪A.
解:集合A={x|x
2+x-6<0}={x|-3<x<2},集合B={x|3x
2-5x-12≤0}={x|
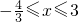
},
则C
RA={x|x≤-3或x≥2},C
RB={x|x<

或x>3}.
所以,C
RA∩B={x|x≤-3或x≥2}∩{x|
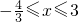
}={x|2≤x≤3};
C
RB∪A={x|x<

或x>3}∪{x|-3<x<2}={x|x<2或x>3}.
分析:通过求解一元二次不等式分别化简集合A和集合B,然后运用交集、并集和补集的运算求解.
点评:本题考查了一元二次不等式的解法,考查了集合的交集与补集的混合运算,是基础题,也是高考常会考查的题型.
