Question

16．甲、乙两楼相距20米，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，求甲、乙两楼的高．

Answer 1

分析 由题意画出图形，过点C作CM⊥AB于点M，根据题意得：CM=BD=20米，∠ACM=30°，∠ADB=60°，然后在Rt△ACM与Rt△ADB中，用正切函数计算即可求得两楼的高度

解答 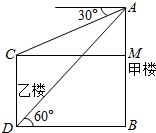解：如图过点C作CM⊥AB于点M，根据题意得：CM=BD=20米，∠ACM=30°，∠ADB=60°，
在Rt△ACM中，tan30°=$\frac{AM}{CM}$=$\frac{\sqrt{3}}{3}$
∴AM=$\frac{\sqrt{3}}{3}$CM=20×$\frac{\sqrt{3}}{3}$=$\frac{20\sqrt{3}}{3}$（米），
在Rt△ADB中，tan60°=$\frac{AB}{BD}$
∴AB=DB•tan60°=20$\sqrt{3}$（米），
CD=AB-AM=20$\sqrt{3}$-$\frac{20\sqrt{3}}{3}$=$\frac{40\sqrt{3}}{3}$（米）
所以甲楼高$20\sqrt{3}$米，乙楼高$\frac{{40\sqrt{3}}}{3}$米

点评 本题考查了应用正弦定理、余弦定理解三角形应用题问题；一般是根据题意，从实际问题中抽象出一个或几个三角形，通过解这些三角形，从而使实际问题得到解决．