
【题目】已知函数![]() 在一个周期内的图象如图所示.
在一个周期内的图象如图所示.
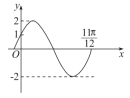
(1)求函数![]() 的解析式.
的解析式.
(2)求方程![]() 的解的个数.
的解的个数.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】我市正在创建全国文明城市,某高中为了解学生的创文知晓率,按分层抽样的方法从“表演社”、“演讲社”、“围棋社”三个活动小组中随机抽取了6人进行问卷调查,各活动小组人数统计如下图:
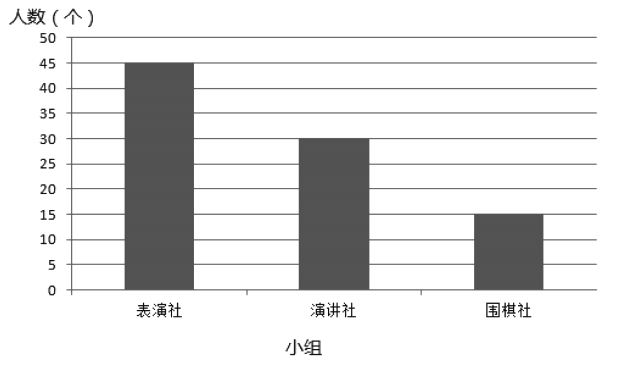

(1)从参加问卷调查的6名学生中随机抽取2名,求这2名学生来自同一小组的概率;
(2)从参加问卷调查的6名学生中随机抽取3名,用![]() 表示抽得“表演社”小组的学生人数,求
表示抽得“表演社”小组的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将编号为1,2,…,9的九个小球随机放置在圆周的九个等分点上,每个等分点上各有一个小球.设圆周上所有相邻两球号码之差的绝对值之和为S.求使S达到最小值的放法的概率.注:如果某种放法经旋转或镜面反射后可与另一种放法重合,则认为是相同的放法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: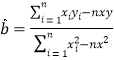 ,
,![]() (精确到
(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月31日,十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定,这是我国个人所得税法自1980年出台以来第七次大修![]() 为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元,则应缴纳的个人所得税为______元![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在函数定义域内,若存在区间![]() ,使得函数值域为
,使得函数值域为![]() ,则称此函数为“
,则称此函数为“![]() 档类正方形函数”,已知函数
档类正方形函数”,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 的最大值是1,求实数
的最大值是1,求实数![]() 的值;
的值;
(3)当![]() 时,是否存在
时,是否存在![]() ,使得函数
,使得函数![]() 为“1档类正方形函数”?若存在,求出实数
为“1档类正方形函数”?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上的
上的![]() 、
、![]() 两点满足
两点满足![]() ,点
,点![]() 、
、![]() 在抛物线对称轴的左右两侧,且
在抛物线对称轴的左右两侧,且![]() 的横坐标小于零,抛物线顶点为
的横坐标小于零,抛物线顶点为![]() ,焦点为
,焦点为![]() .
.
(1)当点![]() 的横坐标为2,求点
的横坐标为2,求点![]() 的坐标;
的坐标;
(2)抛物线上是否存在点![]() ,使得
,使得![]() (
(![]() ),若请说明理由;
),若请说明理由;
(3)设焦点![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() ,求当四边形
,求当四边形![]() 面积最小值时点
面积最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com