Question

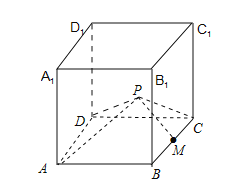
【题目】已知棱长为3的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是侧面DCC1D1内（包括边界）的一个动点，且满足∠APD＝∠MPC.则当三棱锥P﹣BCD的体积最大时，三棱锥P﹣BCD的外接球的表面积为_____.

Answer 1

【答案】21π

【解析】

由题意得三角形相似，再借助函数求最大值，求出的位置在棱上，且时三棱锥的体积最大，然后由三棱锥为一条侧棱垂直于底面的三棱锥，它的外接球的球心是过底面外接圆的圆心做垂直于底面的直线与中截面的交点，而底面为直角三角形，所以底面外接圆的圆心为斜边的中点，且半径为斜边的一半，根据底面外接圆的半径与球的半径和三棱锥的高的一半构成直角三角形，由题意求出外接球的半径，求出外接球的表面积．

由题意得是的中点，点是侧面内（包括边界）的一个动点，

且满足

，，及．

设，，，，

化简得，当时，，

所以点在上，且时三棱锥的体积最大，

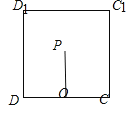
这时底面外接圆圆心为斜边的中点，球心为过垂直于底面的直线与中截面的交点，

则，底面半径，设球的半径，则，，

所以三棱锥的外接球的表面积为，

故答案为：．