设m,n∈R,若直线l:mx+ny-1=0与x轴相交于点A,与y轴相交于点B,且l与圆x2+y2=4相交所得弦的长为2,O为坐标原点,则△AOB面积的最小值为 .
【答案】
分析:由圆的方程找出圆心坐标和半径r,由直线l被圆截得的弦长与半径,根据垂径定理及勾股定理求出圆心到直线l的距离,然后再利用点到直线的距离公式表示出圆心到直线l的距离,两者相等列出关系式,整理后求出m
2+n
2的值,再由直线l与x轴交于A点,与y轴交于B点,由直线l的解析式分别令x=0及y=0,得出A的横坐标及B的纵坐标,确定出A和B的坐标,得出OA及OB的长,根据三角形AOB为直角三角形,表示出三角形AOB的面积,利用基本不等式变形后,将m
2+n
2的值代入,即可求出三角形AOB面积的最小值.
解答:解:由圆x
2+y
2=4的方程,得到圆心坐标为(0,0),半径r=2,
∵直线l与圆x
2+y
2=4相交所得弦CD=2,
∴圆心到直线l的距离d=
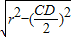
=
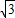
,
∴圆心到直线l:mx+ny-1=0的距离d=
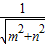
=
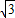
,
整理得:m
2+n
2=

,
令直线l解析式中y=0,解得:x=
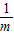
,
∴A(
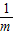
,0),即OA=
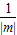
,
令x=0,解得:y=
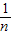
,
∴B(0,
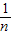
),即OB=
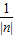
,
∵m
2+n
2≥2|mn|,当且仅当|m|=|n|时取等号,
∴|mn|≤
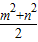
,
又△AOB为直角三角形,
∴S
△ABC=

OA•OB=
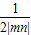
≥
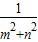
=3,
则△AOB面积的最小值为3.
故答案为:3
点评:此题考查了直线与圆相交的性质,涉及的知识有:点到直线的距离公式,垂径定理,勾股定理,直线的一般式方程,以及基本不等式的运用,当直线与圆相交时,常常根据垂径定理由垂直得中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理俩来解决问题.

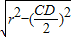 =
=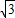 ,
,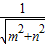 =
=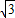 ,
, ,
,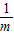 ,
,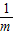 ,0),即OA=
,0),即OA=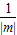 ,
,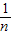 ,
,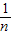 ),即OB=
),即OB=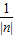 ,
,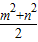 ,
, OA•OB=
OA•OB=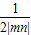 ≥
≥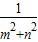 =3,
=3,

 名校课堂系列答案
名校课堂系列答案