
����Ŀ��ij��ȤС�����о���ҹ�²��С�뻼��ð��������֮��Ĺ�ϵ,���Ƿֱ��������ijҽԺ��¼��1��6�·�ÿ��10�ŵ���ҹ�²��������ð�����������,�õ���������:

����ȤС��ȷ�����о�������:����2��3��4��5�µ�4�����������Իع鷽��,����1�º�6�µ�2�����ݽ��м���.
��1�������2��3��4��5�µ�����,���y����x�����Իع鷽��![]() ��
��
��2���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2��,����Ϊ�õ������Իع鷽���������,���ʸ�С���������Իع鷽���Ƿ�����?
���ο���ʽ:  ��
��![]()
 ��
��
�ο����ݣ�11��25+13��29+12��26+8��16=![]() 1092��112+132+122+82=498.
1092��112+132+122+82=498.
���𰸡���1��![]() ����2��������
����2��������
��������
�����������1���������������ݣ����x��y��ƽ���������������Իع鷽��ϵ���ķ��������ϵ��b����b��x��y��ƽ������������a�Ĺ�ʽ������a��ֵ��д�����Իع鷽�̣�
��2��������������Իع鷽�̣�Ԥ�����Ա���Ϊ10��6ʱ��y��ֵ����Ԥ����ֵͬԭ������������10��6��Ӧ��ֵ�����ľ���ֵ������2���õ����Իع鷽�����룮
���������
��1�����������![]()
�ɹ�ʽ���![]()
����![]()
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() .
.
��2����![]() ʱ,
ʱ, ![]() ,
, ![]() ��
��
ͬ��, ��![]() ʱ,
ʱ, ![]() ,
, ![]()
����,��С���������Իع鷽���������.


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��m��R��ʹ�ú���f��x��=x2+��m��1��x2��2���溯��������q������ ![]() =��x1 �� y1����
=��x1 �� y1���� ![]() =��x2 �� y2������
=��x2 �� y2������ ![]() =
= ![]() ���ǣ���
���ǣ��� ![]()
![]() ���ij�Ҫ����������������Ϊ��������ǣ� ��
���ij�Ҫ����������������Ϊ��������ǣ� ��
A.p��q
B.���Vp����q
C.p�ģ��Vq��
D.���Vp���ģ��Vq��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ϵ�����������ֱ������ϵxOy�У�ԲC�IJ������� ![]() ����Ϊ����������OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��
����Ϊ����������OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��
��1����ԲC�ļ����귽�̣�
��2������OM����= ![]() ��ԲC�Ľ���ΪO��P���㣬��P��ļ����꣮
��ԲC�Ľ���ΪO��P���㣬��P��ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������2015�������쳣�𱬣���ij����Ⱥij�ν��е��������У�������������ܽ��Ϊ8Ԫ�����������Ϊ1.72Ԫ��1.83Ԫ��2.28Ԫ��1.55Ԫ��0.62Ԫ�� 5�ݹ��ס��ҵ�5������ÿ��ֻ����һ�Σ���ס��Ҷ��������Ľ��֮�Ͳ�����3Ԫ�ĸ�����
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����רҵ400��ѧ���μ�ij�β�����������Ůѧ������������ʹ�÷ֲ�����ķ������������ȡ��100��ѧ������¼���ǵķ����������ݷֳ�7�飺[20,30����[30,40��������[80,90]���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
���������400��ѧ���������ȡһ�ˣ����������С��70�ĸ��ʣ�
������֪�����з���С��40��ѧ����5�ˣ��Թ��������з���������[40,50���ڵ�������
��������֪��������һ�������ķ�����С��70���������з�����С��70����Ů��������ȣ��Թ���������������Ů�������ı�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() ��������Ϊ
��������Ϊ ![]() ��F����ԲC���ҽ��㣮����F��б��Ϊk��k��0����ֱ��l����ԲC����A��B���㣬O������ԭ�㣮
��F����ԲC���ҽ��㣮����F��б��Ϊk��k��0����ֱ��l����ԲC����A��B���㣬O������ԭ�㣮
��1����n��ֵ��
��2�����߶�AB�Ĵ�ֱƽ������y��Ľؾ�Ϊ ![]() ����k��ֵ��
����k��ֵ��
��3���Ƿ���ڵ�P��t��0����ʹ��PFΪ��APB��ƽ���ߣ������ڣ����t��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��
��![]() ����������Ϊ
����������Ϊ![]() ��
��![]() Ϊ��Բ
Ϊ��Բ![]() ��λ�ڵ�һ�����ڵ�һ��.
��λ�ڵ�һ�����ڵ�һ��.
��1������![]() ������Ϊ
������Ϊ![]() ������Բ
������Բ![]() �ı����̣�
�ı����̣�
��2����![]() Ϊ��Բ
Ϊ��Բ![]() ���㣬
���㣬![]() Ϊ��Բ
Ϊ��Բ![]() ��һ�㣬��
��һ�㣬��![]() ����ֱ��
����ֱ��![]() ��б��.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������P��ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD����E���߶�PC�ϣ�PC��ƽ��BDE��
��1��֤����BD��ƽ��PAC��
��2����PA=1��AD=2��������B��PC��A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD-A1B1C1D1���ⳤΪ1���߶�B1D1������������E��F����EF=![]() �� �����н����д���ĸ�����( )
�� �����н����д���ĸ�����( )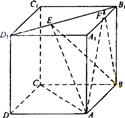
(1) AC��BE.
(2) ��PΪAA1�ϵ�һ��,��P��ƽ��BEF�ľ���Ϊ![]() .
.
(3) ����A-B![]() EF�����Ϊ��ֵ.
EF�����Ϊ��ֵ.
(4) �ڿռ���DD1,AC,B1C1���ཻ��ֱ����������.
(5) ��CC1���е���ֱ��AC1���ɽ�Ϊ40������ƽ��BEF���ɽ�Ϊ50��ֱ����2��.
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com