考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)欲证平面A1DE⊥平面ACC1A1,根据面面垂直的判定定理可知在平面ADE内一直线与平面ACC1A1垂直,而根据DE⊥AA1而DE⊥AE.AA1∩AE=A满足线面垂直的判定定理可知DE⊥平面ACC1A1;
(2)过点A做AF垂直A1E于F,连接DF,由(1)知:平面A1DE⊥平面ACC1A1.所以AF⊥平面A1DE,则∠ADF即为直线AD和平面A1DE所成角,在三角形ADF中求出此角即可.
解答:
解:(1)如图所示,由正三棱柱ABC-A
1B
1C
1的性质知AA
1⊥平面A
1B
1C
1又DE?平面A
1B
1C
1,
所以DE⊥AA
1.
而DE⊥AE.AA
1∩AE=A,
所以DE⊥平面ACC
1A
1,
又DE?平面A
1DE,
故平面A
1DE⊥平面ACC
1A
1.
(2)过点A做AF垂直A
1E于F,连接DF,

由(1)知:平面A
1DE⊥平面ACC
1A
1.
所以AF⊥平面A
1DE,
则∠ADF即为直线AD和平面A
1DE所成角,
因为DE⊥平面ACC
1A
1.
所以DE⊥AC,
而△ABC是边长为4的正三角形,
所以AD=2
,AE=4-CE=4-
CD=3,
又因为AA
1=
,
所以A
1E=
=
=4,
AF=
=
,
所以sin∠ADF=
=
,
故直线AD和平面A
1DE所成角的正弦值为
点评:本小题主要考查空间中的线面关系,考查面面垂直的判定及线面所成角的计算,考查逻辑思维能力、运算能力和推理论证能力,考查转化思想,属于基础题.

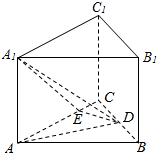 如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=
如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案