
 将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且a1=a13=1,a31=
将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且a1=a13=1,a31=| 5 | 3 |
| n(n+1) |
| 2 |
| 5 |
| 3 |
| n(n+1) |
| 2 |
| 4×5 |
| 2 |
| 7×8 |
| 2 |
| 5 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2n-1 |
| 3n-1 |
(2n-1)(1-
| ||
1-
|
| 3 |
| 2 |
| 3n-1 |
| 3n |
| 1 |
| 3 |
| 2n-1 |
| 3n-1 |
| 1 |
| 1 |
| 3 |
| 3 |
| 5 |
| 32 |
| 2n-1 |
| 3n-1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 32 |
| 5 |
| 33 |
| 2n-1 |
| 3n |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n-1 |
| 2n-1 |
| 3n |
| ||||
1-
|
| 2n-1 |
| 3n |
| 2n+2 |
| 3n |
| n+1 |
| 3n-1 |


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
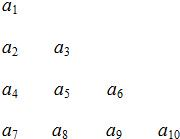 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10…记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10…记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足| 2bn | ||
bnSn-
|
| 1 |
| Sn |
| 4 |
| 91 |
查看答案和解析>>
科目:高中数学 来源:江西省南昌市2011届高三第二次模拟考试数学文科试题 题型:044
将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数![]() 构成数列为{bn},各行的最后一个数
构成数列为{bn},各行的最后一个数![]() 构成数列为{cn},第n行所有数的和为
构成数列为{cn},第n行所有数的和为![]()
![]() .已知数列{dn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且
.已知数列{dn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且![]() .
.
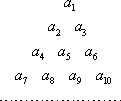
(1)求数列![]() 的通项公式.
的通项公式.
(2)求数列{cn}的前n项和Tn的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
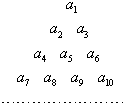 将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且
将正数数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且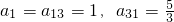 .
.查看答案和解析>>
科目:高中数学 来源:2012年广东省新课程高考冲刺全真模拟数学试卷4(文科)(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com