求周长为定值L(L>0)的直角三角形的面积的最大值.
【答案】
分析:因为L=a+b+c,c=
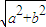
,两次运用均值不等式即可求解;或者利用三角代换,转化为三角函数求最值问题.
解答:解:直角三角形的两直角边为a、b,斜边为c,面积为s,
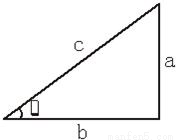
解法一:a+b+
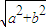
=L≥2
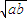
+
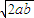
.
∴
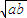
≤
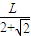
.
∴S=

ab≤

(
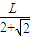
)
2=

•[
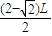
]
2=
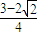
L
2.
解法二:设a=csinθ,b=ccosθ.
∵a+b+c=L,
∴c(1+sinθ+cosθ)=L.
∴c=
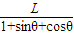
.
∴S=

c
2sinθcosθ=
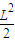
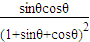
.
设sinθ+cosθ=t∈(1,
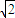
],
则S=
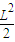
•
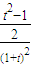
=
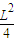
•
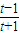
=
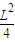
(1-
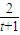
)≤
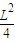
(1-
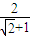
)=
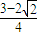
L
2.
点评:利用均值不等式解决实际问题时,列出有关量的函数关系式或方程式是均值不等式求解或转化的关键.
