

图1-3-6
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求DE的长.
思路分析:第(1)问,∵AD=AC,∴∠ACB=∠CDF.又D是BC中点,ED⊥BC,
∴∠B=∠ECD.∴△ABC∽△FCD.
第(2)问利用相似三角形的性质,作AM⊥BC于M,易知S△ABC=4S△FCD.
∴S△ABC=20,AM=4.又∵AM∥ED,∴![]() ,再根据等腰三角形的性质及中点,可以求出DE.也可运用△ABC∽△FCD,由相似比为2,证出F是AD的中点,通过“两三角形等底等高,则面积相等”,求出S△ABC=20.
,再根据等腰三角形的性质及中点,可以求出DE.也可运用△ABC∽△FCD,由相似比为2,证出F是AD的中点,通过“两三角形等底等高,则面积相等”,求出S△ABC=20.
(1)证明:∵DE⊥BC,D是BC中点,∴EB=EC.∴∠B=∠1.
又∵AD=AC,∴∠2=∠ACB.∴△ABC∽△FCD.
(2)解法一:过点A作AM⊥BC,垂足为点M.
∵△ABC∽△FCD,BC=2CD,∴![]() 2=4.
2=4.
又∵S△FCD=5,∴S△ABC=20.
∵S△ABC=![]() BC·AM,BC=10,∴20=
BC·AM,BC=10,∴20=![]() ×10×AM.∴AM=4.
×10×AM.∴AM=4.
又∵DE∥AM,∴![]() .
.
∵DM=![]() DC=
DC=![]() ,BM=BD+DM,BD=
,BM=BD+DM,BD=![]() BC=5,
BC=5,
∴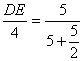 ∴DE=
∴DE=![]() .
.
解法二:作FH⊥BC,垂足为点H.

图1-3-7
∵S△FCD=![]() DC·FH,又∵S△FCD=5,DC=
DC·FH,又∵S△FCD=5,DC=![]() BC=5,
BC=5,
∴5=![]() ×5×FH.∴FH=2.
×5×FH.∴FH=2.
过点A作AM⊥BC,垂足为点M,∵△ABC∽△FCD,
∴![]() =
=![]() .∴AM=4.
.∴AM=4.
又∵FH∥AM,∴![]() =
=![]() =
=![]() .
.
∴点H是DM的中点.
又∵FH∥DE,∴![]() .
.
∵HC=HM+MC=![]() ,∴
,∴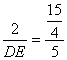 .∴DE=
.∴DE=![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
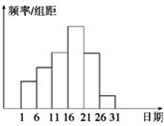 在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2:3:4:6:4:1,第三组的频数为12,则本次活动参加评比作品总数、上交的作品数量最多的组的作品件数依次为( )
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2:3:4:6:4:1,第三组的频数为12,则本次活动参加评比作品总数、上交的作品数量最多的组的作品件数依次为( )| A、60、18 | B、60、20 | C、80、18 | D、80、30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2013届贵州省高二上学期期末考试理科数学 题型:选择题
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图(如图所示),已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在(80,100)之间的学生人数是
A. 32人 B. 27人 C. 24人 D. 33人
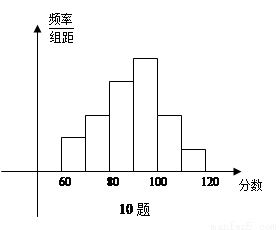
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com