[题目]在一次马拉松比赛中.35名运动员的成绩如图I所示若将运动员按成绩由好到差编为1~35号.再用系统抽样方法从中抽取7人.则其中成绩在区间[139,151]上的运动员人数为( )A.3B.4C.5D.6 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】(2015·湖南）在一次马拉松比赛中，35名运动员的成绩（单位：分钟）如图I所示

若将运动员按成绩由好到差编为1~35号，再用系统抽样方法从中抽取7人，则其中成绩在区间[139,151]上的运动员人数为( )
A.3
B.4
C.5
D.6

【答案】B
【解析】根据茎叶图中的数据，得成绩在区间[139, 151]上的运动员人数是20，用系统抽样方法从35人中抽取7人，成绩在区间[139, 151]上的运动员应抽取7X=4（人）:故选B.
系统抽样是指当总体中个数较多时，将总体分成均衡的几部分，然后按照预先定出的规则，从每一部分抽取1个个体，得到所需要的样本的抽样方法，其实质为等距抽样. 茎叶图的优点是保留了原始数据，便于记录及表示，能反映数据在各段上的分布情况．缺点为不能直接反映总体的分布情况. 由数据集中情况可以估计平均数大小，再根据其分散程度可以估测方差大小．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】

（2015·新课标Ⅱ）设函数f‘（x）是奇函数f（x）（xR）的导函数，f（-1）=0，当x0时，xf'（x）-f（x）0，则使得f（x）0成立的x的取值范围是（）

A.（-，-1）（0，1）
B.（-1，0）（1，+）
C.（-，-1）（-1，0）
D.（0，1）（1，+）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(2015·四川）已知函数f(x)=2x ， g(x)=x2+ax（其中aR）.对于不相等的实数x1, x2 ，设m=，n=.
现有如下命题：
（1）对于任意不相等的实数x1, x2 ，都有m>0；
（2）对于任意的a及任意不相等的实数x1, x2 ，，都有n>0；
（3）对于任意的a ，存在不相等的实数x1, x2 ，使得m=n；
（4）对于任意的a ，存在不相等的实数x1, x2 ，使得m=-n.
其中的真命题有（写出所有真命题的序号）.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(2015·陕西）在直角坐标系xOy中，直线l的参数方程为（t为参数）．以原点为极点，x轴正半轴为极轴建立极坐标系，c的极坐标方程为=2sin ．
（1）写出c的直角坐标方程；
（2）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(2015·江苏）如图，在直三棱柱ABC-A1B1C1中，已知AC⊥BC，BC=CC1 ，设AB1的中点为D，B1CBC1=E.求证:

（1）DE∥平面AA1C1C
（2）BC1⊥AB1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(2015·湖南）设数列{an}的前n项和为Sn ，已知a1=1, a2=2，且an+1=3Sn-Sn+1+3(n)
（1）证明：an+2=3an；
（2）求Sn

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆（a＞b＞0）过点（0，），且离心率为。

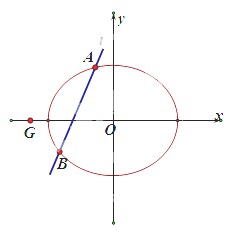
(Ⅰ)求椭圆E的方程；
（II）设直线x my 1,(m R)交椭圆E与A,B两点，判断点G（-,0）与以线段AB为直径的圆的位置关系，并说明理由。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(2015·湖北）某厂用鲜牛奶在某台设备上生产两种奶制品．生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨B产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天B产品的产量不超过A产品产量的2倍，设备每天生产两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为

（Ⅰ）求Z的分布列和均值；该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z（单位：元）是一个随机变量．
（Ⅱ）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．