
 如图,已知三棱柱ABC-A1B1C1中,CA=CB,侧面AA1B1B是菱形,且∠ABB1=60°.
如图,已知三棱柱ABC-A1B1C1中,CA=CB,侧面AA1B1B是菱形,且∠ABB1=60°.分析 (1)取AB中点,连接OC,OB1,证明AB⊥平面OCB1,即可证明.AB⊥B1C;
(2)建立空间坐标系,求出平面的法向量,利用向量法先求出二面角的余弦值,然后求正弦值即可.
解答 解:(1)∵四边形AA1B1B是菱形,且∠ABB1=60°.
∴△ABB1是等边三角形,
取AB中点,连接OC,OB1,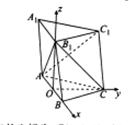 则AB⊥OB1,
则AB⊥OB1,
∵CA=CB,∴AB⊥OC,
∵OC∩OB1=O,OB1,OC?平面OB1C,
∴AB⊥平面OCB1,∴AB⊥B1C;
(2)∵△ABB1是等边三角形,AB=2,∴OB1=$\sqrt{3}$,
∵在△ABC中,AB=2,BC=AC=$\sqrt{2}$,O为AB的中点,
∴OC=1,
∵B1C=2,0B1=$\sqrt{3}$,∴OB12+OC2=B1C2,
∴OB1⊥OC,
∵OB1⊥AB,
∴OB1⊥平面ABC,
以O为坐标原点,OB,OC,OB1的方向为x,y,z轴的正向,建立如图所示的坐标系,
可得A(-1,0,0),B1(0,0,$\sqrt{3}$),B(1,0,0),C(0,1,0),
则$\overrightarrow{O{C}_{1}}$=$\overrightarrow{OC}$+$\overrightarrow{C{C}_{1}}$=$\overrightarrow{OC}$+$\overrightarrow{B{B}_{1}}$=(-1,1,$\sqrt{3}$),则C(-1,1,$\sqrt{3}$),
$\overrightarrow{A{B}_{1}}$=(1,0,$\sqrt{3}$),$\overrightarrow{A{C}_{1}}$=(0,1,$\sqrt{3}$),
则平面BAB1的一个法向量为$\overrightarrow{m}$=(0,1,0),
设$\overrightarrow{n}$=(x,y,z)为平面AB1C1的法向量,
则:$\overrightarrow{n}$•$\overrightarrow{A{B}_{1}}$=x+$\sqrt{3}$z=0,$\overrightarrow{n}$•$\overrightarrow{A{C}_{1}}$=y+$\sqrt{3}$z=0,
令z=-1,则x=y=$\sqrt{3}$,
可得 $\overrightarrow{n}$=($\sqrt{3}$,$\sqrt{3}$,-1),
故cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{21}}{7}$,
则sin<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\sqrt{1-(\frac{\sqrt{21}}{7})^{2}}$=$\frac{2\sqrt{7}}{7}$,
即二面角B-AB1-C1的正弦值是$\frac{2\sqrt{7}}{7}$.
点评 本题主要考查线面垂直的判断以及二面角的求解,根据相应的判定定理以及建立空间坐标系,求出平面的法向量,利用向量法是解决二面角的常用方法.


科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
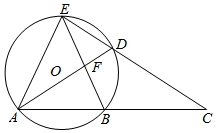 如图,点A、B、D、E在⊙O上,ED、AB的延长线交于点C,AD、BE交于点F,AE=EB=BC.
如图,点A、B、D、E在⊙O上,ED、AB的延长线交于点C,AD、BE交于点F,AE=EB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点E、F分别是正方体ABCD-A1B1C1D1的棱AD、AA1的中点,G是棱CC1上一点.
如图,点E、F分别是正方体ABCD-A1B1C1D1的棱AD、AA1的中点,G是棱CC1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在圆柱OO1中,AB,CD是底面圆O的两条直径,CC1,DD1是圆柱OO1的两条母线,且AC=1,BC=CC1=$\sqrt{3}$.
如图所示,在圆柱OO1中,AB,CD是底面圆O的两条直径,CC1,DD1是圆柱OO1的两条母线,且AC=1,BC=CC1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
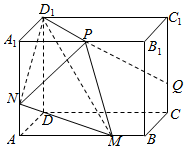 长方体ABCD-A1B1C1D1中,AB=4,AA1=3,BC=2,P为A1B1中点,M,N,Q分别为棱AB,AA1,CC1上的点,且AB=4MB,AA1=3AN,CC1=3CQ.
长方体ABCD-A1B1C1D1中,AB=4,AA1=3,BC=2,P为A1B1中点,M,N,Q分别为棱AB,AA1,CC1上的点,且AB=4MB,AA1=3AN,CC1=3CQ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
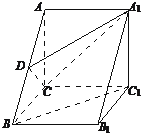 如图,三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1,D为AB的中点,且CD⊥DA1
如图,三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1,D为AB的中点,且CD⊥DA1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
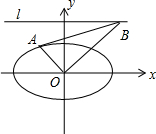 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{\sqrt{2}}{2}$,点A是椭圆C上任意一点,且△AF1F2的周长为2($\sqrt{2}$+1)
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{\sqrt{2}}{2}$,点A是椭圆C上任意一点,且△AF1F2的周长为2($\sqrt{2}$+1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com