Question

11．以下命题中：
①设有一个回归方程$\widehat{y}$=2-3x，变量x增加一个单位时，y平均增加3个单位；
②两个随机变量的线性相关性越强，则相关系数的绝对值越接近于1；
③在某项测量中，测量结果ξ服从正态分布N（1，σ²）（σ＞0）．若ξ在（0，1）内取值的概率为0.4，则ξ在（0，2）内取值的概率为0.8．
④将八进制数135_（8）转化为二进制数是1011101_（2）
其中真命题的个数为（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 ①根据回归方程的性质进行判断．
②根据线性相关系数进行判断．
③根据正态分布的性质进行求解判断．
④根据八进制和二进制之间的关系进行判断即可．

解答 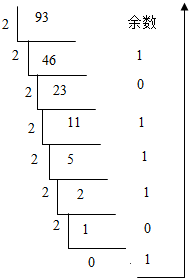解：①设有一个回归方程$\widehat{y}$=2-3x，变量x增加一个单位时，y平均减少3个单位，故①错误；
②根据线性相关系数r的意义可知，当两个随机变量线性相关性越强，r的绝对值越接近于1，故②正确；
③在某项测量中，测量结果ξ服从正态分布N（1，σ²）（σ＞0）．若ξ在（0，1）内取值的概率为0.4，
则ξ在（0，2）内取值的概率P=2×0.4=0.8．故③正确，
④将八进制数135_（8）转化为10进制数，
135_（8）=1×8²+3×8¹+5×8⁰=93_（10）．
利用“除2取余法”可得
93_（10）=1011101_（2）．故④正确，
故真命题的个数为3个，
故选：C

点评 本题考查抽样方法的概念、相关系数的意义以及正态分布的特点和曲线表示的意义，涉及的知识点较多，比较综合．