
【题目】已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)求|MQ|的最大值和最小值;
(2)若M(m,n),求![]() 的最大值和最小值
的最大值和最小值
【答案】(1)6![]() ,2
,2![]() (2)最大值为2+
(2)最大值为2+![]() ,最小值为2-
,最小值为2-![]()
【解析】
试题(1)求圆上的点到定点的距离最值,首先求圆心到直线的距离,再此基础上加减半径得到距离的最大值和最小值;(2)![]() 看作两点
看作两点![]() 连线的斜率,结合图形可知斜率的最值为直线与圆相切时的切线斜率
连线的斜率,结合图形可知斜率的最值为直线与圆相切时的切线斜率
试题解析:(1)由C:x2+y2-4x-14y+45=0可得(x-2)2+(y-7)2=8,
∴圆心C的坐标为(2,7),半径r=2![]() .
.
又|QC|=![]() =4
=4![]() .∴|MQ|max=4
.∴|MQ|max=4![]() +2
+2![]() =6
=6![]() ,
,
|MQ|min=4![]() -2
-2![]() =2
=2![]() .
.
(2)可知![]() 表示直线MQ的斜率,设直线MQ的方程为y-3=k(x+2),
表示直线MQ的斜率,设直线MQ的方程为y-3=k(x+2),
即kx-y+2k+3=0,则![]() =k.由直线MQ与圆C有交点,
=k.由直线MQ与圆C有交点,
所以![]() ≤2
≤2![]() .可得2-
.可得2-![]() ≤k≤2+
≤k≤2+![]() ,
,
所以![]() 的最大值为2+
的最大值为2+![]() ,最小值为2-
,最小值为2-![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】假设国家收购某种农产品的价格是1.2元/kg,其中征税标准为每100元征8元(即税率为8个百分点,8%),计划可收购![]() kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低![]() 个百分点,预计收购可增加
个百分点,预计收购可增加![]() 个百分点.
个百分点.
(1)写出税收![]() (元)与
(元)与![]() 的函数关系;
的函数关系;
(2)要使此项税收在税率调节后不低于原计划的78%,确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,命题
,命题![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=BC=4,BB1=2![]() ,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
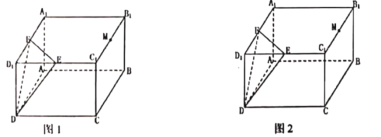
(1)在图1中,画出这个几何图形,并求这个几何图形的面积(不必说明画法与理由)
(2)在图2中,求证:D1B⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新冠肺炎疫情的影响下,南充高中响应“停课不停教,停课不停学”的号召进行线上教学,高二年级的甲乙两个班中,需根据某次数学测试成绩选出某班的5名学生参加数学竞赛决赛,已知这次测试他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
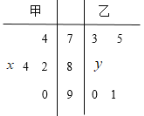
(1)求出x,y的值,且分别求甲乙两个班中5名学生成绩的方差![]() ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com