
【题目】已知函数![]() (
(![]() 且
且![]() )是定义在
)是定义在![]() 上的奇函数.
上的奇函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的值域;
的值域;
(Ⅲ)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|,a<0.
(Ⅰ)证明f(x)+f(﹣ ![]() )≥2;
)≥2;
(Ⅱ)若不等式f(x)+f(2x)< ![]() 的解集非空,求a的取值范围.
的解集非空,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交的作品的件数按5天一组分组统计,绘制了频率分布直方图,如图所示,已知从左到右各长方形的高的比为2 : 3 : 4 : 6 : 4 :1,第三组的频数为12.

(1)求本次活动参加评比的作品的件数;
(2)哪组上交的作品数量最多,有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,函数
,函数![]() .
.
(1)求![]() 的定义域
的定义域![]() 及其零点;
及其零点;
(2)讨论并用函数单调性定义证明函数![]() 在定义域
在定义域![]() 上的单调性;
上的单调性;
(3)设![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在![]() (不含80)之间,属于酒后驾车,在
(不含80)之间,属于酒后驾车,在![]() (含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
酒精含量
|
|
|
|
|
|
|
|
|
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(1)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
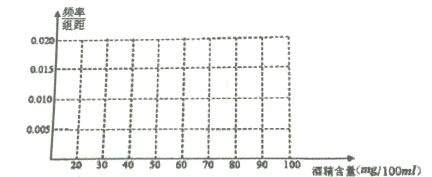
(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x﹣2)2+(y﹣3)2=1交于点M,N两点.
(1)求k的取值范围;
(2)请问是否存在实数k使得 ![]() (其中O为坐标原点),如果存在请求出k的值,并求|MN|;如果不存在,请说明理由.
(其中O为坐标原点),如果存在请求出k的值,并求|MN|;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A , B , C的对边分别为a , b , c , cos ![]() =
= ![]() .
.
(1)求cosB的值;
(2)若 ![]() ,b=2
,b=2 ![]() ,求a和c的值.
,求a和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,直线
中,直线 ![]() 的参数方程为
的参数方程为  (
( ![]() 为参数).再以原点为极点,以
为参数).再以原点为极点,以 ![]() 正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系 ![]() 有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() 、
、 ![]() ,若点
,若点 ![]() 的坐标为
的坐标为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com