
设
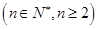 ,
,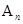 的所有非空子集中的最小元素的和为
的所有非空子集中的最小元素的和为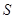 ,则
,则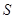 = .
= .
科目:高中数学 来源: 题型:填空题
已知定义在R上的函数f(x),g(x)满足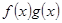 =ax,且f′(x)g(x)+f(x)·g′(x)<0,
=ax,且f′(x)g(x)+f(x)·g′(x)<0,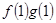 +
+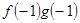 =
=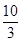 ,若有穷数列{
,若有穷数列{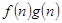 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于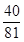 ,则n等于 .
,则n等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
一个数列,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列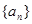 是等和数列,且
是等和数列,且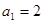 ,公和为5,那么这个数列的前21项和
,公和为5,那么这个数列的前21项和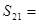 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com