
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2 ![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 ![]() ,求λ的值.
,求λ的值.
【答案】
(1)解:直线AB的方程是y=2 ![]() (x﹣
(x﹣ ![]() ),与y2=2px联立,有4x2﹣5px+p2=0,
),与y2=2px联立,有4x2﹣5px+p2=0,
∴x1+x2= ![]()
由抛物线定义得:|AB|=x1+x2+p=9
∴p=4,∴抛物线方程是y2=8x
(2)解:由p=4,4x2﹣5px+p2=0得:x2﹣5x+4=0,
∴x1=1,x2=4,
y1=﹣2 ![]() ,y2=4
,y2=4 ![]() ,从而A(1,﹣2
,从而A(1,﹣2 ![]() ),B(4,4
),B(4,4 ![]() ).
).
设 ![]() =(x3,y3)=(1,﹣2
=(x3,y3)=(1,﹣2 ![]() )+λ(4,4
)+λ(4,4 ![]() )=(4λ+1,4
)=(4λ+1,4 ![]() λ﹣2
λ﹣2 ![]() )
)
又[2 ![]() (2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2
(2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2
【解析】(1)直线AB的方程与y2=2px联立,有4x2﹣5px+p2=0,从而x1+x2= ![]() ,再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.(2)由p=4,4x2﹣5px+p2=0求得A(1,﹣2
,再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.(2)由p=4,4x2﹣5px+p2=0求得A(1,﹣2 ![]() ),B(4,4
),B(4,4 ![]() ).再求得设
).再求得设 ![]() 的坐标,最后代入抛物线方程即可解得λ.
的坐标,最后代入抛物线方程即可解得λ.


科目:高中数学 来源: 题型:
【题目】一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8, 
(1)求频率分布直方图中a,b的值;
(2)根据频率分布直方图,估计这20棵果树产量的中位数;
(3)根据频率分布直方图,估计这1000棵果树的总产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( ) 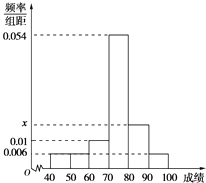
A.75.5
B.75.2
C.75.1
D.75.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中.
(1)设 ![]()
![]() =
= ![]()
![]() ,求证:△ABC是等腰三角形;
,求证:△ABC是等腰三角形;
(2)设向量 ![]() =(2sinC,﹣
=(2sinC,﹣ ![]() ),
), ![]() =(sin2C,2cos2
=(sin2C,2cos2 ![]() ﹣1),且
﹣1),且 ![]() ∥
∥ ![]() ,若sinA=
,若sinA= ![]() ,求sin(
,求sin( ![]() ﹣B)的值.
﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4 ![]() x的交点为椭圆
x的交点为椭圆 ![]() (a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点.
(a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点. 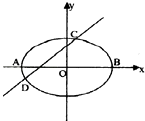
(1)求椭圆标准方程;
(2)求四边形ADBC的面积的最大值;
(3)若M(x1 , y1)N(x2 , y2)是椭圆上的两动点,且满x1x2+2y1y2=0,动点P满足 ![]() (其中O为坐标原点),是否存在两定点F1 , F2使得|PF1|+|PF2|为定值,若存在求出该定值,若不存在说明理由.
(其中O为坐标原点),是否存在两定点F1 , F2使得|PF1|+|PF2|为定值,若存在求出该定值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点.证明A1 , C1 , F,E四点共面,并求直线CD1与平面A1C1FE所成角的正弦值. 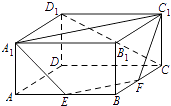
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式exf(x)>ex+1的解集为( )
A.(0,+∞)
B.(﹣∞,0)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x)+f(x+1)=0,且在[﹣3,﹣2]上f(x)=2x+5,A、B是三边不等的锐角三角形的两内角,则下列不等式正确的是( )
A.f(sinA)>f(sinB)
B.f(cosA)>f(cosB)
C.f(sinA)>f(cosB)
D.f(sinA)<f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则14分钟后P点距地面的高度是米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com