
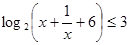 ;
;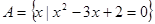 ,
,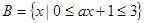 .若
.若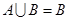 ,求实数
,求实数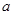 的取值组成的集合.
的取值组成的集合.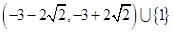 ;(2)
;(2)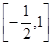 .
.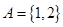 ,由
,由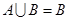 知
知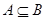 ,要具体化集合
,要具体化集合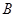 的过程中,要解一个含有参数的不等式,要对参数进行分类讨论,然后对各种情况下的结果利用
的过程中,要解一个含有参数的不等式,要对参数进行分类讨论,然后对各种情况下的结果利用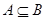 解决问题,较为简单的做法是,集合
解决问题,较为简单的做法是,集合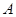 中的元素都在集合
中的元素都在集合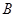 ,都满足不等式,代入即可解决问题.
,都满足不等式,代入即可解决问题.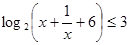 得,
得,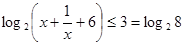
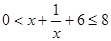 .
. 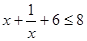 解得
解得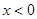 或
或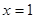
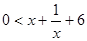 解得
解得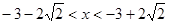 或
或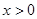
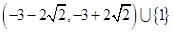 .
.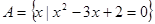
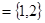 ,
,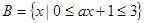
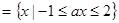 ,
,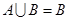 ,∴
,∴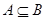
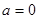 时,
时,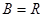 ,满足题意.
,满足题意.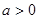 时,
时,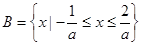 ,∵
,∵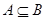 ∴
∴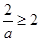 ,解得
,解得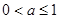 .
.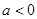 时,
时,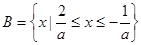 ,∵
,∵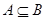 ∴
∴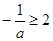 ,解得
,解得 .
.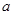 的取值组成的集合为
的取值组成的集合为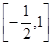 .
.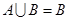 ,∴
,∴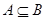
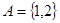 ,∴
,∴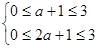 ∴
∴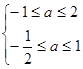 ,∴
,∴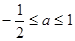 .
.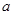 的取值组成的集合为
的取值组成的集合为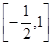 .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com