
【题目】已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.
(1)当x∈[1,2]时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2017)的值.
【答案】(1)f(x)=22-x-1,x∈[1,2];(2)1.
【解析】试题分析:(1) ![]() ;(2) 有对称性和奇偶性可得
;(2) 有对称性和奇偶性可得![]()
![]() 所求
所求![]() .
.
试题解析:
(1)当x∈[1,2]时,2-x∈[0,1],
又f(x)的图象关于x=1对称,
则f(x)=f(2-x)=22-x-1,x∈[1,2].
(2)∵函数f(x)为奇函数,则f(-x)=-f(x),
又函数f(x)的图象关于x=1对称,
则f(2+x)=f(-x)=-f(x),
所以f(4+x)=f[(2+x)+2]=-f(2+x)=f(x),
所以f(x)是以4为周期的周期函数.
∵f(0)=0,f(1)=1,f(2)=0,f(3)=f(-1)=-f(1)=-1,
又f(x)是以4为周期的周期函数.
∴f(0)+f(1)+f(2)+…+f(2017)=504×(0+1+0-1)+f(0)+f(1)=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
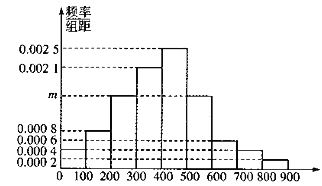
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(Ⅱ)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中![]() 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(参考公式和计算结果: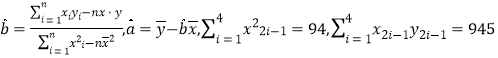 )
)
(Ⅲ)设出油量与勘探深度的比值![]() 不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个正数a,b,可按规则![]() 扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若a=1,b=3,按上述规则操作三次,扩充所得的数是_____________;
(2)若p>q>0,经过6次操作后扩充所得的数为![]() (m,n为正整数),
(m,n为正整数),
则m,n的值分别为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计乙获胜的概率.
先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数.
034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751
据此估计乙获胜的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次战役中,狙击手A受命射击敌机,若要击落敌机,需命中机首2次或命中机中3次或命中机尾1次,已知A每次射击,命中机首、机中、机尾的概率分别为0.2、0.4、0.1,未命中敌机的概率为0.3,且各次射击相互独立。若A至多射击两次,则他能击落敌机的概率为( )
A. 0.23 B. 0.2 C. 0.16 D. 0.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com