【题目】若关于x的不等式|ax﹣2|＜3的解集为{x|﹣ 
＜x＜ 
}，则a= ．
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系 
中，曲线 
的参数方程为 
（其中 
为参数），曲线 
： 
，以坐标原点 
为极点， 
轴的正半轴为极轴建立极坐标系.
（1）求曲线 的普通方程和曲线 的极坐标方程；
（2）若射线 
（ 
）与曲线 ， 分别交于 
， 
两点，求 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】当|a|≤1，|x|≤1时，关于x的不等式|x2﹣ax﹣a2|≤m恒成立，则实数m的取值范围是（ ）
A.[
， +∞）
B.[
， +∞）
C.[
， +∞）
D.[
， +∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对定义域分别是
、
的函数
，
，一个函数
：
.
（Ⅰ）若
，
，写出函数的解析式；
（Ⅱ）在（Ⅰ）的条件下，若
恒成立，求实数
的取值范围；
（Ⅲ）当
，
时，若函数
有四个零点，分别为
，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了
月
日至月
日的每天昼夜温差与实验室每天每
颗种子中的发芽数，得到如下资料：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 |
|
|
|
|
|
发芽数 |
|
|
|
|
|
该农科所确定的研究方案是：先从这组数据中选取
组，用剩下的
组数据求线性回归方程，再用被选取的组数据进行检验.
（1）求选取的组数据恰好是不相邻天的数据的概率；
（2）若选取的是月日与月日的两组数据，请根据月日至
日的数据，求出
关于
的线性回归方程
，由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过颗，则认为得到的线性回归方程是可靠的，试问（2）中所得试的线性回归方程是否可靠？
附：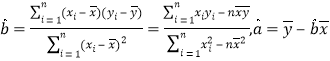
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】用数学归纳法证明12+22+…+（n﹣1）2+n2+（n﹣1）2+…+22+12═ 
时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（ ）
A.（k+1）2+2k2
B.（k+1）2+k2
C.（k+1）2
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，C＝
，a＝5，△ABC的面积为10
.
（1）求b，c的值；
（2）求cos（B－）的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头，它们在一天二十四小时内到达该码头的时刻是等可能的．如果甲船停泊时间为1小时，乙船停泊时间为2小时，求它们中的任意一艘都不需要等待码头空出的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
