
【题目】某机构通过对某企业2018年的前三个季度生产经营情况的调查,得到每月利润![]() (单位:万元)与相应月份数
(单位:万元)与相应月份数![]() 的部分数据如表:
的部分数据如表:
| 3 | 6 | 9 |
| 241 | 244 | 229 |
(1)根据上表数据,请从下列三个函数中选取一个恰当的函数描述![]() 与x的变化关系,并说明理由:
与x的变化关系,并说明理由:![]() ,
,![]() ,
,![]()
(2)利用(1)中选择的函数:
①估计月利润最大的是第几个月,并求出该月的利润;
②预估年底12月份的利润是多少?
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为集合A,g(x)=
的定义域为集合A,g(x)=![]() 的定义域为集合B,C={x
的定义域为集合B,C={x![]() R|x<a或x>a+1}
R|x<a或x>a+1}
(1)求集合A,(C![]() A)
A)![]() B
B
(2)若A![]() C=R,求实数a的取值范围
C=R,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛测试的学生中随机抽出60名学生,将其成绩(百分制)(均为整数)分成六段![]() ,
,![]() …
…![]() 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:

(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,从图中估计总体的众数是多少分?中位数是多少分?
(3)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).

(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据绘制的散点图能够看出可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明;(系数精确到0.001)
加以说明;(系数精确到0.001)
(2)建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
(系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:(1)样本![]() 的相关系数
的相关系数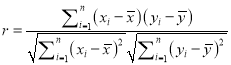
(2)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为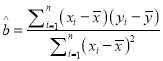 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 若![]() ,则“
,则“![]() ”的充分条件是“
”的充分条件是“![]() ”
”
B. 若![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
C. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
D. ![]() 是等比数列,则
是等比数列,则![]() 是
是![]() 为单调递减数列的充分条件
为单调递减数列的充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张矩形白纸ABCD,AB=10,AD=![]() ,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)
,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)

①当平面ABE∥平面CDF时,AC∥平面BFDE
②当平面ABE∥平面CDF时,AE∥CD
③当A、C重合于点P时,PG⊥PD
④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com