
| A. | $\overrightarrow{AB}=\overrightarrow{DC}$ | B. | $\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AC}$ | C. | $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{BD}$ | D. | $\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{BD}$ |
分析 根据相等向量的定义,及向量加法和向量减法的平行四边形法则,逐一分析四个式子的正误,可得答案.
解答 解:在平行四边形ABCD中,
向量$\overrightarrow{AB}与\overrightarrow{DC}$方向相同,大小相等,故$\overrightarrow{AB}=\overrightarrow{DC}$,故A正确;
根据向量加法的平行四边形法则,可得$\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AC}$,故B正确;
根据向量减法的平行四边形法则,可得$\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}$,故C错误;
根据向量加法的平行四边形法则,可得$\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BD}$,故D正确;
故选:C.
点评 本题考查的知识点是向量加法和向量减法的平行四边形法则,相等向量的定义,难度不大,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$+π | B. | $\frac{2}{3}$+2π | C. | $\frac{8}{3}$+8π | D. | $\frac{4}{3}$+4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{2}{3},+∞)$ | B. | (1,+∞) | C. | $[{\frac{2}{3},1}]$ | D. | $(\frac{2}{3},\left.1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
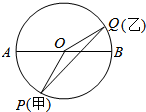 如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.
如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com