
分析 由题意,转化为(x+y-z)(y+z-x)(z+x-y)>0,由对称性不妨设x≥y≥z,则有x+y-z≥x>0,z+x-y≥z>0,得到y+z-x>0,即可证明.
解答 证明:$\frac{{x}^{2}+{y}^{2}-{z}^{2}}{2xy}$+$\frac{{y}^{2}+{z}^{2}-{x}^{2}}{2yz}$+$\frac{{z}^{2}+{x}^{2}-{y}^{2}}{2zx}$>1,x>0,y>0,z>0,两边同乘以2xyz,
∴z(x2+y2-z2)+x(y2+z2-x2)+y(z2+x2-y2)>2xyz,
∴zx2+zy2-z3+xy2+xz2-x3+yz2+yx2-y3-2xyz>0,
∴(x+y-z)(y+z-x)(z+x-y)>0,
由对称性不妨设x≥y≥z,则有x+y-z≥x>0,z+x-y≥z>0,
∴y+z-x>0,
∴x,y,z是某个三角形的三边的长.
点评 本题考查了不等式的性质和三角形的两边之和大于第三边,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | k≥4或k≤-4 | B. | $k≥\sqrt{2}$或$k≤-2\sqrt{2}$ | C. | $k=±2\sqrt{3}$ | D. | $k=±2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -11 | B. | 46 | C. | 77 | D. | -76 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
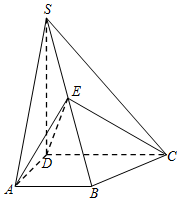 如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com