
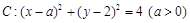 及直线
及直线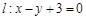 . 当直线
. 当直线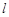 被圆
被圆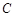 截得的弦长为
截得的弦长为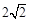 时, 求(1)
时, 求(1)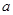 的值; (2)求过点
的值; (2)求过点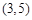 并与圆
并与圆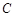 相切的切线方程.
相切的切线方程. ;(2)
;(2) 或
或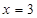
 的距离
的距离 ,可列式为
,可列式为 ,进而求
,进而求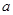 ;(2)先利用点斜式方程设直线为
;(2)先利用点斜式方程设直线为 ,因为直线和圆相切,利用
,因为直线和圆相切,利用 求参数
求参数 ,因为点
,因为点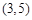 在圆外,所以切线可引两条,则会想到另一条直线必是斜率不存在 情况,再补
在圆外,所以切线可引两条,则会想到另一条直线必是斜率不存在 情况,再补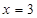 .
.
 ,则圆心到直线
,则圆心到直线 的距离
的距离 ,由勾股定理可知
,由勾股定理可知 ,代入化简得
,代入化简得 ,解得
,解得 ,又
,又 ,所以
,所以 ;
;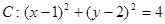 , 又
, 又 在圆外,
在圆外, ①当切线方程的斜率存在时,设方程为
①当切线方程的斜率存在时,设方程为 ,由圆心到切线的距离
,由圆心到切线的距离 可解得
可解得 ,
, 切线方程为
切线方程为 ……9分,②当过
……9分,②当过 斜率不存在,易知直线
斜率不存在,易知直线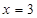 与圆相切,综合①②可知切线方程为
与圆相切,综合①②可知切线方程为 或
或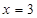 .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com