
一个函数f(x),如果对任 意一 个三 角形 ,只要它的三边长a,b,c都在f(x)的定 义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给 出下 列函 数:① f(x)=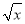 ,②
,②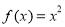 ;③f(x)=2x ;④f(x)=?lg x ,其中是“三角保型函数”的是( )
;③f(x)=2x ;④f(x)=?lg x ,其中是“三角保型函数”的是( )
A.①② B.①③ C.②③④ D.③④
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在△ABC中,角A,B,C所对的边依次为a,b,c,已知a=bcosC+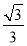 csinB
csinB
(1)求B;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试理科数学试卷(解析版) 题型:解答题
一企业某次招聘新员工分笔试和面试两部分,人力资源部经理把参加笔试的 40 名学生的成绩分组: 第 1 组[75,80),第 2 组 [80,85),第 3 组[85, 90),第 4 组 [90, 95),第 5 组[95,100),得到频率分布直方图如图所示:
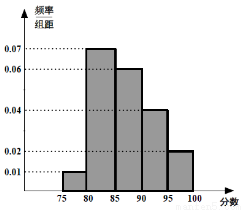
(1)分别求成绩在第 4,5 组的人数;
(2)若该经理决定在笔试成绩较高的第 3,4,5 组中用分层抽样抽取 6 名进入面试,
①已知甲和乙的成绩均在第 3 组,求甲和乙同时进入面试的概率;
②若经理决定在这 6 名学生中随机抽取 2 名学生接受考官 D 的面试,设第 4 组中有 X 名学生被考官 D 面试,求 X 的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:解答题
已知数列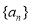 是公差大于零的等差数列,数列
是公差大于零的等差数列,数列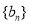 为等比数列,且
为等比数列,且 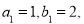
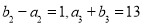
(1)求数列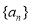 和
和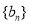 的通项公式
的通项公式
(2)设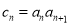 ,求数列
,求数列 前n项和
前n项和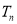 .
.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:选择题
已知曲线  在点 P(1,4)处的切线与直线 l 平行且距离为
在点 P(1,4)处的切线与直线 l 平行且距离为 ,则直线 l 的方程为( )
,则直线 l 的方程为( )
A. 或
或
B.
C. 或
或
D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2015届北京市海淀区高三上学期期中练习文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数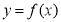 ,
,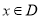 ,设曲线
,设曲线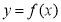 在点
在点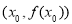 处的切线方程为
处的切线方程为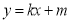 . 如果对任意的
. 如果对任意的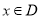 ,均有:
,均有:
①当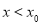 时,
时,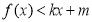 ;
;
②当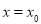 时,
时, ;
;
③当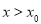 时,
时,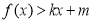 ,
,
则称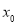 为函数
为函数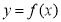 的一个“? -点”.
的一个“? -点”.
(1)判断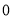 是否是下列函数的“? -点”:
是否是下列函数的“? -点”:
①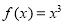 ; ②
; ②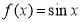 .(只需写出结论)
.(只需写出结论)
(2)设函数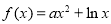 .
.
(ⅰ)若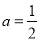 ,证明:
,证明: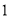 是函数
是函数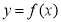 的一个“? -点”;
的一个“? -点”;
(ⅱ)若函数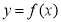 存在“? -点”,直接写出
存在“? -点”,直接写出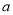 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com