
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() ,设圆
,设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)联立直线![]() 与直线
与直线![]() ,求得圆心坐标,根据
,求得圆心坐标,根据![]() 点坐标设出切线的方程,由圆心到切线的距离等于圆的半径,列出关于
点坐标设出切线的方程,由圆心到切线的距离等于圆的半径,列出关于![]() 的方程,求出方程的解得
的方程,求出方程的解得![]() 的值,确定出切线方程即可;(2)设圆心
的值,确定出切线方程即可;(2)设圆心![]() 为
为![]() ,则圆
,则圆![]() 的方程为:
的方程为:![]() ,利用两点间的距离公式列出关系式,得出圆的方程,由
,利用两点间的距离公式列出关系式,得出圆的方程,由![]() 在圆
在圆![]() 上,得到圆
上,得到圆![]() 与圆
与圆![]() 相交或相切,根据两圆的半径长,得出两圆的圆心的距离的范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到
相交或相切,根据两圆的半径长,得出两圆的圆心的距离的范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到![]() 的范围.
的范围.
试题解析:(1)由![]() 得圆心
得圆心![]() 为(3,2),∵圆
为(3,2),∵圆![]() 的半径为
的半径为![]()
∴圆![]() 的方程为:
的方程为:![]()
显然切线的斜率一定存在,设所求圆C的切线方程为![]() ,即
,即![]()
∴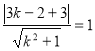 ∴
∴![]() ∴
∴![]() ∴
∴![]() 或者
或者![]()
∴所求圆C的切线方程为:![]() 或者
或者![]() 即
即![]() 或者
或者![]()
(2)∵圆![]() 的圆心在在直线
的圆心在在直线![]() 上,所以,设圆心
上,所以,设圆心![]() 为
为![]() ,
,
则圆![]() 的方程为:
的方程为:![]()
又∵![]() ∴设M为(x,y)则
∴设M为(x,y)则![]() 整理得:
整理得:![]() 设为圆
设为圆![]()
∴点M应该既在圆![]() 上又在圆
上又在圆![]() 上,即圆
上,即圆![]() 和圆
和圆![]() 有交点
有交点
∴![]()
由![]() 得
得![]()
由![]() 得
得![]()
终上所述,![]() 的取值范围为
的取值范围为![]()


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别是B,D,如果增加一个条件,就能推出BD⊥EF,这个条件不可能是下面四个选项中的 ( )
A. AC⊥β
B. AC⊥EF
C. AC与BD在β内的射影在同一条直线上
D. AC与α,β所成的角相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的![]() 个小球,其中有红色球
个小球,其中有红色球![]() 个,编号分别为
个,编号分别为![]() ;白色球
;白色球![]() 个, 编号分别为
个, 编号分别为![]() , 从盒子中任取
, 从盒子中任取![]() 个小球(假设取到任何—个小球的可能性相同).
个小球(假设取到任何—个小球的可能性相同).
(1)求取出的![]() 个小球中,含有编号为
个小球中,含有编号为![]() 的小球的概率;
的小球的概率;
(2)在取出的![]() 个小球中, 小球编号的最大值设为
个小球中, 小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间生产一种仪器的固定成本是![]() 元,每生产一台该仪器需要增加投入
元,每生产一台该仪器需要增加投入![]() 元,已知总收入满足函数:
元,已知总收入满足函数: ,其中
,其中![]() 是仪器的月产量.
是仪器的月产量.
(利润=总收入-总成本).
(1)将利润表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条。假定这种围巾的销售量t(条)是售价x(元)(![]() )的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(![]() )的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润-总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面说法正确的有
①演绎推理是由一般到特殊的推理;
②演绎推理得到的结论一定是正确的;
③演绎推理的一般模式是三段论;
④演绎推理的结论的正误与大前提、小前提和推理形式有关.
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com