
【题目】方程 ![]() 在(0,2π)内有相异两解α,β,则α+β=
在(0,2π)内有相异两解α,β,则α+β=
【答案】![]() 或
或 ![]()
![]()
【解析】解:∵sinx+ ![]() cosx+a=0,
cosx+a=0,
∴﹣a=sinx+ ![]() cosx=2(
cosx=2( ![]() sinx+
sinx+ ![]() cosx)=2sin(x+
cosx)=2sin(x+ ![]() ),
),
令f(x)=2sin(x+ ![]() ),y=﹣a,
),y=﹣a,
∵0<x<2π,
∴ ![]() <x+
<x+ ![]() <2π+
<2π+ ![]() =
= ![]() ,
,
在同一坐标系中作出f(x)=2sin(x+ ![]() )与y=﹣a的图象,
)与y=﹣a的图象,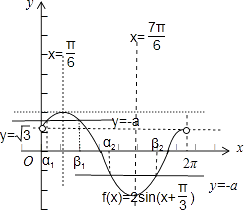
由图知,当x= ![]() ,即x+
,即x+ ![]() =
= ![]() 时,f(x)取到最大值2,当x=
时,f(x)取到最大值2,当x= ![]() 时,x+
时,x+ ![]() =
= ![]() +
+ ![]() =
= ![]() ,f(x)取到最小值﹣2;
,f(x)取到最小值﹣2;
方程sinx+ ![]() cosx+a=0在(0,2π)内有相异两解α,β直线y=﹣a与曲线f(x)=2sin(x+
cosx+a=0在(0,2π)内有相异两解α,β直线y=﹣a与曲线f(x)=2sin(x+ ![]() )在(0,2π)内有两个不同的交点,
)在(0,2π)内有两个不同的交点,
当交点的横坐标分别为α1与β1时,α1+β1= ![]() ;
;
当交点的横坐标分别为α2与β2时,α2+β2= ![]() ;
;
∴α+β= ![]() 或
或 ![]() .
.
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】掌握两角和与差的正弦公式和函数的零点与方程根的关系是解答本题的根本,需要知道两角和与差的正弦公式:![]() ;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是![]() ,
, ![]() 是
是![]() 的中点.
的中点.
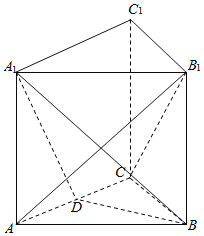
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题
①“若![]() ,则互为相反数”的逆命题;
,则互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“不等边三角形的三个内角相等”的逆命题.
其中真命题为_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
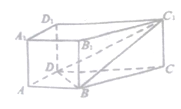
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,若存在实数
,若存在实数![]() 使得一条曲线与直线
使得一条曲线与直线![]() 由两个不同的交点,且以这两个交点为端点的线段长度恰好等于
由两个不同的交点,且以这两个交点为端点的线段长度恰好等于![]() ,则称此曲线为直线
,则称此曲线为直线![]() 的“绝对曲线”.下面给出的四条曲线方程:
的“绝对曲线”.下面给出的四条曲线方程:
①![]() ;②
;② ![]() ;③
;③![]() ;④
;④![]() .
.
其中直线![]() 的“绝对曲线”的条数为( )
的“绝对曲线”的条数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com