
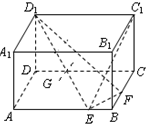
 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E,F分别是棱AB,BC上的点,且EB=FB=1.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E,F分别是棱AB,BC上的点,且EB=FB=1.
| ||
| 11 |
| D1E |
| D1F |
| n |
| ||
| 11 |

| EC1 |
| FD1 |
| EC1 |
| FD1 |
| 6-4+4 | ||||
|
| ||
| 14 |
| D1E |
| D1F |
| n |
| n |
| D1E |
| n |
| D1F |
|
| n |
| EG |
| ||
| 11 |
| |a-3+b-3| | ||
|
| ||
| 11 |
| ||
| 11 |


科目:高中数学 来源: 题型:
 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )查看答案和解析>>
科目:高中数学 来源: 题型:

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:填空题
(文科做)(本题满分14分)如图,在长方体
ABCD—A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC-D的大小为 .
.

(理科做)(本题满分14分)
如图,在直三棱柱ABC – A1B1C1中,∠ACB = 90°,CB = 1,
CA = ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.
(Ⅰ)求证:AM⊥平面A1BC;
(Ⅱ)求二面角B – AM – C的大小;
(Ⅲ)求点C到平面ABM的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com