
【题目】对于不重合的两个平面![]() 与
与![]() ,给定下列条件:
,给定下列条件:
①存在平面![]() ,使得
,使得![]() 、
、![]() 都垂直于
都垂直于![]() ;
;
②存在平面![]() ,使得
,使得![]() 、
、![]() 都平行于
都平行于![]() ;
;
③![]() 内有不共线的三点到
内有不共线的三点到![]() 的距离相等;
的距离相等;
④存在异面直线![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]()
其中,可以判定![]() 与
与![]() 平行的条件有( )
平行的条件有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,∠PAC=∠BAC=90°,PA=PB,点D,F分别为BC,AB的中点.

(1)求证:直线DF∥平面PAC;
(2)求证:PF⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知任意角
中,已知任意角![]() 以坐标原点
以坐标原点![]() 为顶点,
为顶点,![]() 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点![]() ,且
,且![]() ,定义:
,定义:![]() ,称“
,称“![]() ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数![]() ”,有同学得到以下性质:
”,有同学得到以下性质:
①该函数的值域为![]() ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;
③该函数的图象关于直线![]() 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为![]() ;
;
⑤该函数的递增区间为![]() .
.
其中正确的是__________.(填上所有正确性质的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA= ![]() ,连接CE并延长交AD于F
,连接CE并延长交AD于F 
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为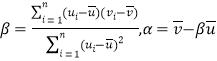 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年投入固定成本![]() 万元.此外,每生产
万元.此外,每生产![]() 件这种产品还需要增加投入
件这种产品还需要增加投入![]() 万元.经测算,市场对该产品的年需求量为
万元.经测算,市场对该产品的年需求量为![]() 件,且当出售的这种产品的数量为
件,且当出售的这种产品的数量为![]() (单位:百件)时,销售所得的收入约为
(单位:百件)时,销售所得的收入约为![]() (万元).
(万元).
(1)若该公司这种产品的年产量为![]() (单位:百件),试把该公司生产并销售这种产品所得的年利润
(单位:百件),试把该公司生产并销售这种产品所得的年利润![]() 表示为年产量
表示为年产量![]() 的函数;
的函数;
(2)当该公司的年产量![]() 为多少时,当年所得利润
为多少时,当年所得利润![]() 最大?最大为多少?
最大?最大为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(0,1),(3+2![]() ,0),(3-2
,0),(3-2![]() ,0)在圆C上.
,0)在圆C上.
(1)求圆C的方程.
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润. 
(1)将T表示为x的函数;
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈[100,110))则取x=105,且x=105的概率等于需求量落入[100,110)的频率,求T的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.y=f(x)的图象关于(π,0)中心对称
B.y=f(x)的图象关于x= ![]() 对称
对称
C.f(x)的最大值为 ![]()
D.f(x)既是奇函数,又是周期函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com