
【题目】已知顶点为原点的抛物线C的焦点与椭圆![]() 的上焦点重合,且过点
的上焦点重合,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若抛物线上不同两点A,B作抛物线的切线,两切线的斜率![]() ,若记AB的中点的横坐标为m,AB的弦长
,若记AB的中点的横坐标为m,AB的弦长![]() ,并求
,并求![]() 的取值范围.
的取值范围.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】关于函数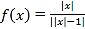 ,给出以下四个命题:(1)当
,给出以下四个命题:(1)当![]() 时,
时,![]() 单调递减且没有最值;(2)方程
单调递减且没有最值;(2)方程![]() 一定有实数解;(3)如果方程
一定有实数解;(3)如果方程![]() (
(![]() 为常数)有解,则解得个数一定是偶数;(4)
为常数)有解,则解得个数一定是偶数;(4)![]() 是偶函数且有最小值.其中假命题的序号是____________.
是偶函数且有最小值.其中假命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,定义椭圆C的“相关圆”E为:
,定义椭圆C的“相关圆”E为:![]() .若抛物线
.若抛物线![]() 的焦点与椭圆C的右焦点重合,且椭圆C的短轴长与焦距相等.
的焦点与椭圆C的右焦点重合,且椭圆C的短轴长与焦距相等.
(1)求椭圆C及其“相关圆”E的方程;
(2)过“相关圆”E上任意一点P作其切线l,若l 与椭圆![]() 交于A,B两点,求证:
交于A,B两点,求证:![]() 为定值(
为定值(![]() 为坐标原点);
为坐标原点);
(3)在(2)的条件下,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的长轴长与焦距比为2:1,左焦点F(﹣2,0),一定点为P(﹣8,0).
(1)求椭圆E的标准方程;
(2)过P的直线与椭圆交于P1、P2两点,设直线P1F、P2F的斜率分别为k1、k2,求证:k1+k2=0.
(3)求△P1P2F面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:

(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量![]() ,及松树数量
,及松树数量![]() 关于n的表达式
关于n的表达式
(2)定义:![]()
![]() 为
为![]() 增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
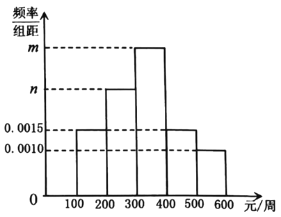
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com