
解析:方法一:设圆心C的坐标为(a,b),半径为r,由题设知圆C截x轴所得劣弧所对的圆心角为90°,圆C截x轴所得弦长为![]() r,所以r=
r,所以r=![]() |b|.?
|b|.?
又截y轴所得的弦长为2,所以r2=a2+1.所以2b2-a2=1.?
圆心C(a,b)到直线l:x-2y=0的距离![]() 即5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,当且仅当a=b时取等号,此时5d2=1,从而d取最小值.?
即5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,当且仅当a=b时取等号,此时5d2=1,从而d取最小值.?
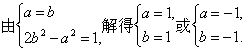
于是有r=![]() .
.
所求圆的方程为(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.?
方法二:由方法一,得![]()
所以a-2b=±![]() d,a=2b±
d,a=2b±![]() d.
d.
代入2b2-a2=1,得2b2±4![]() bd+5d2+1=0.(*)?
bd+5d2+1=0.(*)?
将其视为关于b的一元二次方程,因为b∈R,?
所以Δ=8(5d2-1)≥0,即5d2≥1.?
从而d有最小值![]() .代入(*)式,?
.代入(*)式,?
解得b=±1,a=±1,余下同方法一.


科目:高中数学 来源:2014届浙江省温州市高二第一次月考文科数学试卷(解析版) 题型:解答题
已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1;③圆心到直线l:x-2y=0的距离为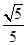 ,求圆的方程.
,求圆的方程.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省卫辉市高三一月月考数学理卷 题型:解答题
(本小题满分13分)
已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1;
③圆心到直线l:x-2y=0的距离为 ,求该圆的方程.
,求该圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com