【题目】东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元，固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本
与科技成本的投入次数
的关系是=
.若水晶产品的销售价格不变,第次投入后的年利润为
万元.①求出的表达式；②问从今年算起第几年利润最高？最高利润为多少万元？
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】设椭圆
(a>b>0)的左焦点为F，上顶点为B. 已知椭圆的离心率为
，点A的坐标为
，且
.
（I）求椭圆的方程；
（II）设直线l： 
与椭圆在第一象限的交点为P，且l与直线AB交于点Q. 若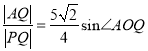
(O为原点) ，求k的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校为担任班主任的教师办理手机语音月卡套餐，为了解通话时长，采用随机抽样的方法，得到该校100位班主任每人的月平均通话时长
（单位：分钟）的数据，其频率分布直方图如图所示，将频率视为概率.
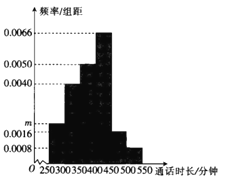
（1）求图中
的值；
（2）估计该校担任班主任的教师月平均通话时长的中位数；
（3）在
，
这两组中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求抽取的2人恰在同一组的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在平行四边形
中，
点
是
边的中点，将
沿
折起，使点
到达点
的位置，且
（1）求证; 平面
平面
；
（2）若平面
和平面
的交线为
，求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，平面
平面ABCD，
是等边三角形，四边形ABCD是矩形，
，F为棱PA上一点，且
，M为AD的中点，四棱锥的体积为
．
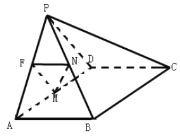
（1）若
，N是PB的中点，求证：平面
平面PCD；
（2）在（Ⅰ）的条件，求三棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若存在实数
使得
则称
是区间
的
一内点．
（1）求证：
的充要条件是存在
使得是区间
的一内点；
（2）若实数
满足：
求证：存在，使得
是区间
的一内点；
（3）给定实数
，若对于任意区间，
是区间的
一内点，
是区间的
一内点，且不等式
和不等式
对于任意
都恒成立，求证：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】禽流感一直在威胁我们的生活，某疾病控制中心为了研究禽流感病毒繁殖个数
（个）随时间
（天）变化的规律，收集数据如下：
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数
的周围.
保留小数点后两位数的参考数据：
，
，
，
，
，
，
，
，其中
（1）求出关于的回归方程（保留小数点后两位数字）；
（2）已知
，估算第四天的残差.
参考公式：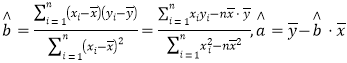
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
