
°ĺŐ‚ńŅ°Ņ°įĹŕ‘ľ”√ňģ°Ī◊‘ĻŇ“‘ņīĺÕ «÷–Ľ™√Ů◊ŚĶń”ŇŃľīęÕ≥£ģń≥ –Õ≥ľ∆ĺ÷Ķų≤ťŃňł√ –÷ŕ∂ŗľ“Õ•Ķń”√ňģŃŅ«ťŅŲ£¨Ľś÷∆Ńň‘¬”√ňģŃŅĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨»ÁŌ¬Õľňý ĺ£ģĹꑬ”√ňģŃŅ¬š»Žłų◊ťĶń∆Ķ¬ ”ő™łŇ¬ £¨≤ĘľŔ…Ť√ŅŐžĶń”√ňģŃŅŌŗĽ•∂ņŃĘ£ģ

£®l£©«ů‘ŕőīņīѨ–Ý3łŲ‘¬ņÔ£¨”–Ѩ–Ý2łŲ‘¬Ķń‘¬”√ňģŃŅ∂ľ≤ĽĶÕ”ŕ12∂÷«“ŃŪ1łŲ‘¬Ķń‘¬”√ňģŃŅĶÕ”ŕ4∂÷ĶńłŇ¬ £Ľ
£®2£©”√![]() ĪŪ ĺ‘ŕőīņī3łŲ‘¬ņÔ‘¬”√ňģŃŅ≤ĽĶÕ”ŕ12∂÷Ķń‘¬ ż£¨«ůňśŤĽĪšŃŅ
ĪŪ ĺ‘ŕőīņī3łŲ‘¬ņÔ‘¬”√ňģŃŅ≤ĽĶÕ”ŕ12∂÷Ķń‘¬ ż£¨«ůňśŤĽĪšŃŅ![]() Ķń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻ
Ķń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻ![]() £ģ
£ģ
°ĺīūįł°Ņ£®1£©0.027£Ľ£®2£©ľŻĹ‚őŲ
°ĺĹ‚őŲ°Ņ∑÷őŲ£ļ£®1£©ņŻ”√ŌŗĽ•∂ņŃĘ ¬ľĢ≥ň∑®łŇ¬ Ļę ĹļÕĽ•≥‚ ¬ľĢľ”∑®Ļę Ĺń‹«ů≥Ų‘ŕőīņīѨ–Ý3łŲ‘¬ņÔ£¨”–Ѩ–Ý2łŲ‘¬Ķń‘¬”√ňģŃŅ∂ľ≤ĽĶÕ”ŕ12∂÷«“ŃŪ1łŲ‘¬Ķń‘¬”√ňģŃŅĶÕ”ŕ4∂÷ĶńłŇ¬ £Ľ
£®2£©”…Ő‚“‚Ķ√XĶńŅ…ń‹»°÷Ķő™0£¨1£¨2£¨3£¨«“X°ę£®3£¨0.3£©£¨”…īňń‹«ů≥ŲňśĽķĪšŃŅXĶń∑÷≤ľŃ– ż—ß∆ŕÕŻE£®X£©£ģ
ŌÍĹ‚£ļ£®1£©…Ť![]() ĪŪ ĺ ¬ľĢ°į‘¬”√ňģŃŅ≤ĽĶÕ”ŕ12∂÷°Ī£¨
ĪŪ ĺ ¬ľĢ°į‘¬”√ňģŃŅ≤ĽĶÕ”ŕ12∂÷°Ī£¨![]() ĪŪ ĺ ¬ľĢ°į‘¬”√ňģŃŅĶÕ”ŕ4∂÷°Ī£¨
ĪŪ ĺ ¬ľĢ°į‘¬”√ňģŃŅĶÕ”ŕ4∂÷°Ī£¨![]() ĪŪ ĺ ¬ľĢ°į‘ŕőīņīѨ–Ý3łŲ‘¬ņÔ£¨”–Ѩ–Ý2łŲ‘¬Ķń‘¬”√ňģŃŅ∂ľ≤ĽĶÕ”ŕ12∂÷«“ŃŪ1łŲ‘¬Ķń‘¬”√ňģŃŅĶÕ”ŕ4∂÷°Ī.
ĪŪ ĺ ¬ľĢ°į‘ŕőīņīѨ–Ý3łŲ‘¬ņÔ£¨”–Ѩ–Ý2łŲ‘¬Ķń‘¬”√ňģŃŅ∂ľ≤ĽĶÕ”ŕ12∂÷«“ŃŪ1łŲ‘¬Ķń‘¬”√ňģŃŅĶÕ”ŕ4∂÷°Ī.
“Úīň£¨![]() £¨
£¨![]() .
.
“Úő™√ŅŐžĶń”√ňģŃŅŌŗĽ•∂ņŃĘ£¨
ňý“‘![]() .
.
£®2£©![]() Ņ…ń‹»°Ķń÷Ķő™0,1,2,3£¨
Ņ…ń‹»°Ķń÷Ķő™0,1,2,3£¨
Ōŗ”¶ĶńłŇ¬ ∑÷Īūő™

![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ļ ![]() Ķń∑÷≤ľŃ–ő™
Ķń∑÷≤ľŃ–ő™
Ļ ![]() Ķń ż—ß∆ŕÕŻő™
Ķń ż—ß∆ŕÕŻő™![]()
![]() .
.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() £¨
£¨
(1)–ī≥ŲňŁĶń’Ů∑ý°Ę÷‹∆ŕ°Ę≥űŌŗ£Ľ
(2)”√°įőŚĶ„∑®°Ī◊ų≥ŲňŁ‘ŕ“ĽłŲ÷‹∆ŕńŕĶńÕľŌů£Ľ
(3)ňĶ√ų![]() ĶńÕľŌůŅ…”…
ĶńÕľŌůŅ…”…![]() ĶńÕľŌůĺ≠Ļż‘ű—ýĶńĪšĽĽ∂ÝĶ√ĶĹ°£
ĶńÕľŌůĺ≠Ļż‘ű—ýĶńĪšĽĽ∂ÝĶ√ĶĹ°£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő™Ńň—–ĺŅń≥÷÷Ōłĺķňś ĪľšxĪšĽĮ£¨∑Ī÷≥ĶńłŲ ż£¨ ’ľĮ żĺ›»ÁŌ¬£ļ
![]()
£®1£©”√Őž ż◊ųĹ‚ ÕĪšŃŅ£¨∑Ī÷≥łŲ ż◊ų‘§Ī®ĪšŃŅ£¨◊ų≥Ų’‚–© żĺ›Ķń…ĘĶ„Õľ£¨łýĺ›…ĘĶ„ÕľŇ–∂Ō£ļ![]() ”Žy=
”Žy=![]() ńń“ĽłŲ◊ųő™∑Ī÷≥ĶńłŲ żyĻō”ŕ ĪľšxĪšĽĮĶńĽōĻť∑Ĺ≥Őņŗ–Õő™◊Óľ—£Ņ£®łÝ≥ŲŇ–∂ŌľīŅ…£¨≤ĽĪōňĶ√ųņŪ”…£©
ńń“ĽłŲ◊ųő™∑Ī÷≥ĶńłŲ żyĻō”ŕ ĪľšxĪšĽĮĶńĽōĻť∑Ĺ≥Őņŗ–Õő™◊Óľ—£Ņ£®łÝ≥ŲŇ–∂ŌľīŅ…£¨≤ĽĪōňĶ√ųņŪ”…£©
|
|
|
|
|
|
3.5 | 62£ģ83 | 3.53 | 17.5 | 596.505 | 12.04 |
∆š÷–![]() £Ľ
£Ľ![]()
£®2£©łýĺ›£®1£©ĶńŇ–∂Ō◊Óľ—ĹŠĻŻľįĪŪ÷–Ķń żĺ›£¨Ĺ®ŃĘyĻō”ŕx ĶńĽōĻť∑Ĺ≥Ő°£
≤őŅľĻę Ĺ£ļ 
![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ŰĻō”ŕxĶń ĶŌĶ ż∑Ĺ≥Őx2+ax+b=0”–ŃĹłŲłý£¨“ĽłŲłý‘ŕ«Ýľš£®0£¨1£©ńŕ£¨ŃŪ“Ľłý‘ŕ«Ýľš£®1£¨3£©ńŕ£¨ľ«Ķ„£®a£¨b£©∂‘”¶Ķń«Ý”Úő™S£ģ
£®1£©…Ťz=2a©Āb£¨«ůzĶń»°÷Ķ∑∂őߣĽ
£®2£©ĻżĶ„£®©Ā5£¨1£©Ķń“Ľ ÝĻ‚ŌŖ£¨…šĶĹx÷ŠĪĽ∑ī…šļůĺ≠Ļż«Ý”ÚS£¨«ů∑ī…šĻ‚ŌŖňý‘ŕ÷ĪŌŖlĺ≠Ļż«Ý”ÚSńŕĶń’ŻĶ„£®ľīļŠ◊›◊ÝĪÍő™’Ż żĶńĶ„£© Ī÷ĪŌŖlĶń∑Ĺ≥Ő£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő“ĻķĻŇīķ ż—ß÷Ý◊ų°∂ĺŇ’¬ň„ ű°∑”…»ÁŌ¬ő Ő‚£ļ°įĹŮ”–ĹūĻ䣨≥§őŚ≥Ŗ£¨’∂Īĺ“Ľ≥Ŗ£¨÷ōňńĹÔ£ģ’∂ń©“Ľ≥Ŗ£¨÷ō∂ĢĹÔ£ģő īő“Ľ≥Ŗłų÷ōľłļő£Ņ°Ī“‚ňľ «£ļ°įŌ÷”–“ĽłýĹū’»£¨≥§5≥Ŗ£¨“ĽÕ∑ī÷£¨“ĽÕ∑Ōł£¨‘ŕī÷Ķń“Ľ∂ňĹōŌ¬1≥Ŗ£¨÷ō4ĹÔ£Ľ‘ŕŌłĶń“Ľ∂ňĹōŌ¬1≥Ŗ£¨÷ō2ĹÔ£Ľő “ņīő√Ņ“Ľ≥Ŗłų÷ō∂ŗ…ŔĹÔ£Ņ°Ī…Ťł√Ĺū’»”…ī÷ĶĹŌł «ĺý‘»ĪšĽĮĶń£¨∆š÷ōŃŅő™![]() £¨Ō÷Ĺęł√Ĺū’»Ĺō≥…≥§∂»ŌŗĶ»Ķń10∂ő£¨ľ«Ķŕ
£¨Ō÷Ĺęł√Ĺū’»Ĺō≥…≥§∂»ŌŗĶ»Ķń10∂ő£¨ľ«Ķŕ![]() ∂őĶń÷ōŃŅő™
∂őĶń÷ōŃŅő™![]() £¨«“
£¨«“![]() £¨»Ű
£¨»Ű![]() £¨‘Ú
£¨‘Ú![]() £® £©
£® £©
A. 6 B. 5 C. 4 D. 7
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńņ‚◊∂P-ABCD÷–£¨AB//CD£¨«“![]()

£®1£©÷§√ų£ļ∆Ĺ√śPAB°Õ∆Ĺ√śPAD£Ľ
£®2£©»ŰPA=PD=AB=DC, ![]() ,«“ňńņ‚◊∂P-ABCDĶńŐŚĽżő™
,«“ňńņ‚◊∂P-ABCDĶńŐŚĽżő™![]() £¨«ůł√ňńņ‚◊∂Ķń≤ŗ√śĽż.
£¨«ůł√ňńņ‚◊∂Ķń≤ŗ√śĽż.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ń∂Ń»ÁÕľĶń≥Ő–ÚŅÚÕľ£¨ š≥ŲĹŠĻŻSĶń÷Ķő™£® £© 
A.©Ā1008
B.1
C.©Ā1
D.0
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥÷÷÷≤‘į‘ŕ√ĘĻŻŃŔĹŁ≥… ž Ī£¨ňśĽķī”“Ľ–©√ĘĻŻ ų…Ō’™Ō¬100łŲ√ĘĻŻ£¨∆š÷ ŃŅ∑÷Īū‘ŕ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £®Ķ•őĽ£ļŅň£©÷–£¨ĺ≠Õ≥ľ∆Ķ√∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁÕľňý ĺ.
£®Ķ•őĽ£ļŅň£©÷–£¨ĺ≠Õ≥ľ∆Ķ√∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁÕľňý ĺ.
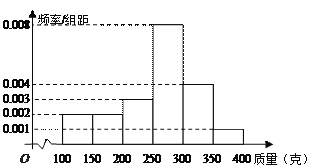
(1) ‘Ļņľ∆’‚◊ť żĺ›Ķń÷ŕ ż°Ę÷–őĽ ż°Ę∆Ĺĺý ż£Ľ
(2)ń≥ĺ≠Ōķ…Őņī ’Ļļ√ĘĻŻ£¨“‘łų◊ť żĺ›Ķń÷–ľš żīķĪŪ’‚◊ť żĺ›Ķń∆Ĺĺý÷Ķ£¨”√—ýĪĺĻņľ∆◊‹ŐŚ£¨ł√÷÷÷≤‘į÷–ĽĻőī’™Ō¬Ķń√ĘĻŻīů‘ľĽĻ”–![]() łŲ£¨ĺ≠Ōķ…ŐŐŠ≥Ų»ÁŌ¬ŃĹ÷÷ ’Ļļ∑Ĺįł£ļ
łŲ£¨ĺ≠Ōķ…ŐŐŠ≥Ų»ÁŌ¬ŃĹ÷÷ ’Ļļ∑Ĺįł£ļ
A£ļňý”–√ĘĻŻ“‘![]() ‘™/«ßŅň ’Ļļ£Ľ
‘™/«ßŅň ’Ļļ£Ľ
B£ļ∂‘÷ ŃŅĶÕ”ŕ![]() ŅňĶń√ĘĻŻ“‘
ŅňĶń√ĘĻŻ“‘![]() ‘™/łŲ ’Ļļ£¨łŖ”ŕĽÚĶ»”ŕ
‘™/łŲ ’Ļļ£¨łŖ”ŕĽÚĶ»”ŕ![]() ŅňĶń“‘
ŅňĶń“‘![]() ‘™/łŲ ’Ļļ.
‘™/łŲ ’Ļļ.
Õ®Ļżľ∆ň„»∑∂®÷÷÷≤‘į—°‘Ůńń÷÷∑ĹįłĽŮņŻłŁ∂ŗ£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() ő™ŇľļĮ ż£ģ
ő™ŇľļĮ ż£ģ
(ĘŮ)«ů![]() Ķń◊Ó–°÷Ķ£Ľ
Ķń◊Ó–°÷Ķ£Ľ
(ĘÚ)»Ű≤ĽĶ» Ĺ![]() ļ„≥…ŃĘ£¨«ů Ķ ż
ļ„≥…ŃĘ£¨«ů Ķ ż![]() Ķń◊Ó–°÷Ķ.
Ķń◊Ó–°÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com