
【题目】已知函数 ![]() .
.
(1)当a=3时,求函数 ![]() 在
在 ![]() 上的最大值和最小值;
上的最大值和最小值;
(2)函数 ![]() 既有极大值又有极小值,求实数a的取值范围.
既有极大值又有极小值,求实数a的取值范围.
【答案】
(1)解:a=3时, ![]() ,
,
函数 ![]() 在区间
在区间 ![]() 仅有极大值点x=1,故这个极大值点也是最大值点,
仅有极大值点x=1,故这个极大值点也是最大值点,
故函数在区间 ![]() 最大值是
最大值是 ![]() ,
,
又 ![]() ,故
,故 ![]() .
.
故函数在 ![]() 上的最小值为
上的最小值为 ![]()
(2)解: ![]()
若 ![]() 既有极大值又有极小值,则
既有极大值又有极小值,则 ![]() 有两个不同正根
有两个不同正根 ![]() ,即
,即 ![]() 有两个不同正根,故a应满足
有两个不同正根,故a应满足 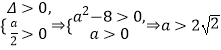
【解析】(1)将a=3代入f(x)中并求出f![]() (x),根据“当f
(x),根据“当f![]() (x)
(x)![]() 0(
0(![]() 0)时,函数f(x)单调递增(减)”确定函数f(x)在[
0)时,函数f(x)单调递增(减)”确定函数f(x)在[![]() ,2]内的单调性,从而可求出f(x)的最大值,比较f(
,2]内的单调性,从而可求出f(x)的最大值,比较f(![]() ),f(2)的大小,进而可求出f(x)的最小值;(2)求出f(x)的定义域,求导,若f(x)既有极大值又有极小值,则f
),f(2)的大小,进而可求出f(x)的最小值;(2)求出f(x)的定义域,求导,若f(x)既有极大值又有极小值,则f![]() (x)=0有两个不同正根,列出不等式组即可求解.
(x)=0有两个不同正根,列出不等式组即可求解.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)计算f(3),f(4),f( ![]() )及f(
)及f( ![]() )的值;
)的值;
(2)由(1)的结果猜想一个普遍的结论,并加以证明;
(3)求值f(1)+f(2)+…+f(2017)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A(n)表示正整数n的个位数,an=A(n2)﹣A(n),A为数列{an}的前202项和,函数f(x)=ex﹣e+1,若函数g(x)满足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.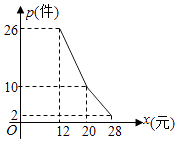
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
①当切线在两坐标轴上的截距为零时,设切线方程为y=kx,
则 ![]() ,解得k=2±
,解得k=2± ![]() ,
,
从而切线方程为y=(2± ![]() )x.
)x.
②当切线在两坐标轴上的截距不为零时,设切线方程为x+y-a=0,则 ![]() ,解得a=-1或3,
,解得a=-1或3,
从而切线方程为x+y+1=0或x+y-3=0.
综上,切线方程为(2+ ![]() )x-y=0或(2-
)x-y=0或(2- ![]() )x-y=0或x+y+1=0或x+y-3=0
)x-y=0或x+y+1=0或x+y-3=0
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com