
分析 (Ⅰ)由条件利用三角恒等变换,化简函数的解析式,再根据正弦函数的周期性,求得函数f(x)的最小正周期
(Ⅱ)由条件利用正弦函数的单调性,求得函数f(x)的单调增区间.
解答 (Ⅰ)解:$f(x)=cosx(sinx+\sqrt{3}cosx)-\frac{{\sqrt{3}}}{2}$=$sinxcosx+\frac{{\sqrt{3}}}{2}(2{cos^2}x-1)$=$\frac{1}{2}sin2x+\frac{{\sqrt{3}}}{2}cos2x$
=$sin(2x+\frac{π}{3})$,
所以函数f(x)的最小正周期$T=\frac{2π}{2}=π$.
(Ⅱ)解:由$2kπ-\frac{π}{2}≤2x+\frac{π}{3}≤2kπ+\frac{π}{2}$,k∈Z,求得$kπ-\frac{5π}{12}≤x≤kπ+\frac{π}{12}$,
所以函数f(x)的单调递增区间为$[kπ-\frac{5π}{12},kπ+\frac{π}{12}]$,k∈Z.
所以当x∈(0,π)时,f(x)的增区间为$(0,\frac{π}{12}]$,$[\frac{7π}{12},π)$.
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{b^2}{a}$ | B. | $\frac{b^2}{c}$ | C. | $\frac{c^2}{a}$ | D. | $\frac{c^2}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,∠ABC=90°,AB=3,BC=4,点O为BC的中点,以BC为直径的半圆与AC,AO分别相交于点M,N,则AN=$\sqrt{13}-2$;$\frac{AM}{MC}$=$\frac{9}{16}$.
如图,在△ABC中,∠ABC=90°,AB=3,BC=4,点O为BC的中点,以BC为直径的半圆与AC,AO分别相交于点M,N,则AN=$\sqrt{13}-2$;$\frac{AM}{MC}$=$\frac{9}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{2}$) | B. | (-$\frac{π}{2}$,$\frac{π}{2}$) | C. | (-π,0) | D. | (0,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
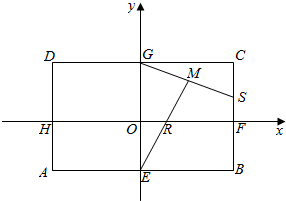 矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.
矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com