
分析 由$\sqrt{3}$c=2asinC,利用正弦定理,可得2sinAsinC=$\sqrt{3}$sinC,求角A,利用ABC的面积,再利用余弦定理,即可求b+c的大小.
解答 解:由$\sqrt{3}$c=2asinC,得2sinAsinC=$\sqrt{3}$sinC,
∵sinC≠0,∴sinA=$\frac{\sqrt{3}}{2}$
又∵△ABC是锐角△,
∴A=$\frac{π}{3}$,
∵△ABC的面积为2$\sqrt{3}$,
∴$\frac{1}{2}bc•\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴bc=8,
∵12=b2+c2-bc,
∴b2+c2=20,
∴(b+c)2=36
∴b+c=6,
故答案为6.
点评 本题考查正弦定理、余弦定理的运用,考查学生的计算能力,正确运用正弦定理、余弦定理是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 销售单价/万元 | [8,10) | [10,12) | [12,14) | [14,16) | [16,18) | [18,20] |
| 频数/辆 | 5 | 10 | 20 | a | 20 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
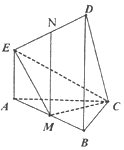 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com