练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，已知sinA=13sinBsinC，cosA=13cosBcosC，则tanA+tanB+tanC的值为 ．

    【答案】196
    【解析】解：∵cosA，cosB，cosC均不为0，由sinA=13sinBsinC①，cosA=13cosBcosC②，

    得：tanA=tanBtanC，

    ∵cosA=13cosBcosC，且cosA=﹣cos（B+C）=sinAsinB﹣cosAcosB，

    ∴sinAsinB=14cosAcosB，

    ∴tanBtanC=14，

    ∵tanB+tanC=tan（B+C）（1﹣tanBtanC）=﹣tanA（1﹣tanBtanC）=﹣tanA+tanAtanBtanC，

    ∴tanA+tanB+tanC=tanAtanBtanC=196．

    所以答案是：196．

    【考点精析】本题主要考查了同角三角函数基本关系的运用的相关知识点，需要掌握同角三角函数的基本关系：；;（3） 倒数关系：才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，焦点在x轴的椭圆，离心率e= ，且过点A（﹣2，1），由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点（Q点与P点不重合）．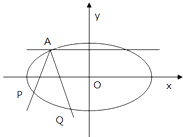

    （1）求椭圆标准方程；
    （2）求证：直线PQ的斜率为定值；
    （3）求△OPQ的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，三棱柱ABC﹣A1B1C1中，已知AB⊥侧面BB1C1C，AB=BC=1，BB1=2，∠BCC1=60°．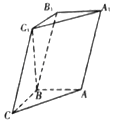

    （Ⅰ）求证：C1B⊥平面ABC；
    （Ⅱ）E是棱CC1所在直线上的一点，若二面角A﹣B1E﹣B的正弦值为 ，求CE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面四边形ABCD中，已知∠A= ，∠B= ，AB=6．在AB边上取点E使得BE=1，连结EC，ED，若∠CED= ，EC= ．则CD= ．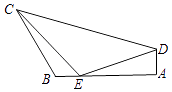

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BCAE=DCAF，B，E，F，C四点共圆．证明：CA是△ABC外接圆的直径．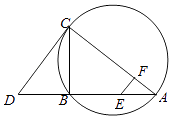

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b是正实数，设函数f（x）=xlnx，g（x）=﹣a+xlnb．
    （Ⅰ）设h（x）=f（x）﹣g（x），求h（x）的单调区间；
    （Ⅱ）若存在x0 ， 使x0∈[ ， ]且f（x0）≤g（x0）成立，求 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3 （1﹣a）x2﹣3ax+1，a＞0．
    （1）试讨论f（x）（x≥0）的单调性；
    （2）证明：对于正数a，存在正数p，使得当x∈[0，p]时，有﹣1≤f（x）≤1；
    （3）设（1）中的p的最大值为g（a），求g（a）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的首项a1=m，其前n项和为Sn ， 且满足Sn+Sn+1=3n2+2n，若对n∈N+ ， an＜an+1恒成立，则m的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的多面体ABCDEF中，ABCD为直角梯形，AB∥CD，∠DAB=90°，四边形ADEF为等腰梯形，EF∥AD，已知AE⊥EC，AB=AF=EF=2，AD=CD=4．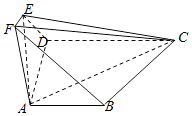

    （1）求证：平面ABCD⊥平面ADEF；
    （2）求直线CF与平面EAC所成角的正弦值．

    查看答案和解析>>

    同步练习册答案