
【题目】抛物线C1:y=![]() x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2:![]() -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】某大型电器企业,为了解组装车间职工的生活情况,从中随机抽取了![]() 名职工进行测试,得到频数分布表如下:
名职工进行测试,得到频数分布表如下:
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
(1)现从参与测试的日组装个数少于![]() 的职工中任意选取
的职工中任意选取![]() 人,求至少有
人,求至少有![]() 人日组装个数少于
人日组装个数少于![]() 的概率;
的概率;
(2)由频数分布表可以认为,此次测试得到的日组装个数![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组数据用该组区间的中点值作为代表).
人得分的平均值(同一组数据用该组区间的中点值作为代表).
(![]() 名职工,求日组装个数超过
名职工,求日组装个数超过![]() 的职工人数;
的职工人数;
(ii)为鼓励职工提高技能,企业决定对日组装个数超过![]() 的职工日工资增加
的职工日工资增加![]() 元,若在组装车间所有职工中任意选取
元,若在组装车间所有职工中任意选取![]() 人,求这三人增加的日工资总额的期望.
人,求这三人增加的日工资总额的期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
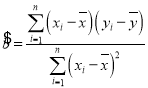 ,,
,,![]() 相关系数
相关系数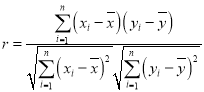
参考数据: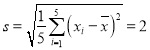 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C1:y=![]() x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2:![]() -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若函数![]() 在
在![]() 上是增函数,求正数
上是增函数,求正数![]() 的取值范围;
的取值范围;
(2)当![]() 时,设函数
时,设函数![]() 的图象与x轴的交点为
的图象与x轴的交点为![]() ,
,![]() ,曲线
,曲线![]() 在
在![]() ,
,![]() 两点处的切线斜率分别为
两点处的切线斜率分别为![]() ,
,![]() ,求证:
,求证:![]() +
+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全社会推行素质教育的大前提下,更强调了学生的全面发展,只有全面重视体育锻炼,才能使学生德智体美全面发展。为了解某高校大学生的体育锻炼情况,做了如下调查统计。该校共有学生10000人,其中男生6000人,女生4000人。为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这200个样本数据,得到学生每周平均体育运动时间的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,估计该校学生每周平均体育运动时间超过4个小时的概率.
,估计该校学生每周平均体育运动时间超过4个小时的概率.
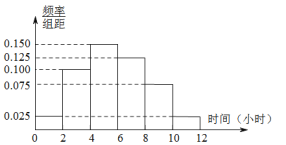
(3)在样本数据中,有50位女生的每周平均体育运动时间超过4个小时,请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“该校学生的每周平均体育运动时间与性别有关”.
女生 | 男生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附:![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
使用手机 | 不使用手机 | 总计 | |
学习成绩优秀 | 10 | 40 | |
学习成绩一般 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
(2)现从上表中不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,求其中学习成绩优秀的学生恰有2人的概率.
参考公式: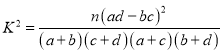 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程
的参数方程![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com