
分析 f′(x)=2cos2x-$\sqrt{3}$,令f′(x)=0,利用单调性与极值的定义可得:xn=$\frac{π}{12}$+(n-1)π(n∈N*).即可判断出①②正确;又θn=$\frac{nπ}{12}$+$\frac{n(n-1)π}{2}$,sinθ1>sinθ2,即可判断出③的正误;由sin(θn+12)=-sinθn,可知:T=12使得对于任意正整数n,都有sinθn=sinθn+T=0成立.即可判断出④的正误.由sinθ18=1,可知n取所有的正整数,sinθn的最大值为1.即可判断出⑤正误.
解答 解:f′(x)=2cos2x-$\sqrt{3}$,令f′(x)=0,利用单调性与极值的定义可得:xn=$\frac{π}{12}$+(n-1)π(n∈N*).因此①②正确;
又θn=x1+x2+…+xn=$\frac{nπ}{12}$+$\frac{n(n-1)π}{2}$,sinθ1>sinθ2,因此③不正确;
由sin(θn+12)=$sin(\frac{(n+12)π}{12}+\frac{(n+12)(n+11)π}{2})$=-$sin(\frac{nπ}{12}+\frac{n(n-1)π}{2})$=-sinθn,可知:T=12使得对于任意正整数n,都有sinθn=sinθn+T=0成立.因此④正确.由sinθ18=1,可知n取所有的正整数,sinθn的最大值为1.因此⑤正确.
故答案为:①②④⑤.
点评 本题考查了三角函数的图象与性质、利用导数研究函数的单调性极值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
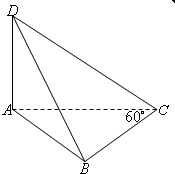 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com