
【题目】设集合A={x|2a﹣1≤x≤a+3},集合B={x|x<﹣1或x>5}.
(1)当a=﹣2时,求A∩B;
(2)若AB,求实数a的取值范围.
【答案】
(1)解当a=﹣2时,A={x|﹣5≤x≤1},集合B={x|x<﹣1或x>5},
∴A∩B={x|﹣5≤x<﹣1}
(2)解∵AB,分两种情况;
当A=,2a﹣1>a+3,解得a>4,
当A≠,则 ![]() 或
或 ![]() ,
,
解得a≤﹣4或a≥3,
综上a的取值范围是{a|a≤﹣4或a≥3}
【解析】(1)根据集合的交集的定义即可求出;(2)由AB的关系,然后分B为空集和非空集合列式求解实数a的取值范围.
【考点精析】根据题目的已知条件,利用集合的交集运算的相关知识可以得到问题的答案,需要掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


科目:高中数学 来源: 题型:
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
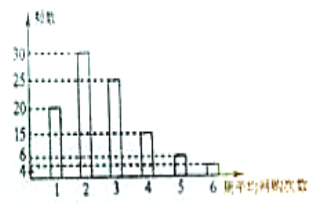
(1)根据已知条件完成下面的![]() 列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
网购迷 | 非网购迷 | 合计 | |
年龄不超过40岁 | |||
年龄超过40岁 | |||
合计 |
(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数![]() 的分布列与期望.
的分布列与期望.
附: 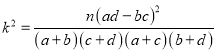 ;
;
| 0.15 | 0.10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣1,1),则函数g(x)=f( ![]() )+f(x﹣1)的定义域为( )
)+f(x﹣1)的定义域为( )
A.(﹣2,0)
B.(﹣2,2)
C.(0,2)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)为奇函数,且在(﹣∞,0)内是减函数,f(2)=0,则 ![]() <0的解集为( )
<0的解集为( )
A.(﹣2,0)∪(2,+∞)
B.(﹣∞,2)∪(0,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0)∪(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足:a7=a6+2a5 , 若存在两项am , an , 使得aman=16a12 , 则 ![]() +
+ ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.不存在
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x|﹣1<x<2},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com