Question

18．已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2，$\overrightarrow{b}$⊥（2$\overrightarrow{a}$-$\overrightarrow{b}$），求|t$\overrightarrow{b}$+（1-2t）$\overrightarrow{a}$|（t∈R）的最小值．

Answer 1

分析 分别作出令$\overrightarrow{AB}$=$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，由条件可得CD⊥AD，再令$\overrightarrow{BH}$=$\overrightarrow{a}$+t（$\overrightarrow{b}$-2$\overrightarrow{a}$），由图形可得当BH⊥CD时，|t$\overrightarrow{b}$+（1-2t）$\overrightarrow{a}$|最小，再由中位线定理，可得最小值．

解答 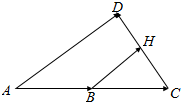解：∵|$\overrightarrow{b}$|=2，$\overrightarrow{b}$⊥（2$\overrightarrow{a}$-$\overrightarrow{b}$），
∴$\overrightarrow{b}$•（2$\overrightarrow{a}$-$\overrightarrow{b}$）=0，
令$\overrightarrow{AB}$=$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，CD⊥AD，
由t$\overrightarrow{b}$+（1-2t）$\overrightarrow{a}$=$\overrightarrow{a}$+t（$\overrightarrow{b}$-2$\overrightarrow{a}$），
令$\overrightarrow{BH}$=$\overrightarrow{a}$+t（$\overrightarrow{b}$-2$\overrightarrow{a}$），
当BH⊥CD时，|t$\overrightarrow{b}$+（1-2t）$\overrightarrow{a}$|最小，
由B为中点，且AD∥BH，
则BH为中位线，且为$\frac{1}{2}$AD=$\frac{1}{2}$×2=1，
故最小值为1．

点评 本题主要考查两个向量的加减法的法则，以及几何意义，向量的模的定义，求向量的模的方法，体现了数形结合的数学思想，属于中档题．