
【题目】已知数集![]() (
(![]() ,
,![]() )具有性质
)具有性质![]() :对任意的
:对任意的![]() 、
、![]() (
(![]() ),
),![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)证明:当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
【答案】(1)数集具有性质P,理由见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)由定义直接判断(2)由已知得anan与![]() 中至少有一个属于A,从而得到a1=1;再由1=a1<a2<…<an,得到akanA(k=2,3,…,n).由A具有性质P可知
中至少有一个属于A,从而得到a1=1;再由1=a1<a2<…<an,得到akanA(k=2,3,…,n).由A具有性质P可知![]() ∈A(k=1,2,3,…,n),由此能证明a1=1,且
∈A(k=1,2,3,…,n),由此能证明a1=1,且![]() an(3)当n=5时,
an(3)当n=5时,![]() ,从而a3a4∈A,
,从而a3a4∈A,![]() ∈A,由此能证明
∈A,由此能证明![]() ,故成等比数列.
,故成等比数列.
(1)由于3×4与![]() 均不属于数集{1,3,4},
均不属于数集{1,3,4},
所以数集{1,3,4}不具有性质P.
由于1×2,1×3,1×6,2×3,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都属于数集{1,2,3,6},
都属于数集{1,2,3,6},
所以数集{1,2,3,6}具有性质P.
(2)证明:
因为A={a1,a2,…,an}具有性质P,
所以anan与![]() 中至少有一个属于A.
中至少有一个属于A.
由于1≤a1<a2<…<an,所以anan>an,故ananA,
从而1![]() ∈A,故a1=1;
∈A,故a1=1;
因为1=a1<a2<…<an,所以akan>an,故akanA(k=2,span>3,…,n).
由A具有性质P可知![]() ∈A(k=1,2,3,…,n),
∈A(k=1,2,3,…,n),
又因为![]() ,
,
所以![]() a1,
a1,![]() ,…,
,…,![]() ,
,![]() ,
,
从而![]() a1+a2+…+an﹣1+an,
a1+a2+…+an﹣1+an,
故a1=1,且![]() an.
an.
(3)证明:
由(2)知,当n=5时,有![]() a2,
a2,![]() ,即
,即![]() ,
,
因为1=a1<a2<…<a5,
所以a3a4>a2a4=a5,故a3a4∈A,
由A具有性质P,可知![]() ∈A,
∈A,
由![]() ,得
,得![]() ∈A,且1
∈A,且1![]() a3,
a3,
所以![]() a2,
a2,
故![]() ,
,
所以![]() ,
,
故![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图,直角梯形![]() 与等腰直角三角形
与等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]() ,
,![]() ,
,![]() ,
,![]() .
.
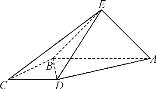
(1) 求证:![]() ;
;
(2) 求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]()
![]() 若存在,求出
若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在D上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在D内恒成立,则称P点为函数
在D内恒成立,则称P点为函数![]() 的“类对称中心点”,则函数
的“类对称中心点”,则函数![]() 的“类对称中心点”的坐标是________.
的“类对称中心点”的坐标是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为![]() 元,低于
元,低于![]() 箱按原价销售,不低于
箱按原价销售,不低于![]() 箱则有以下两种优惠方案:①以
箱则有以下两种优惠方案:①以![]() 箱为基准,每多
箱为基准,每多![]() 箱送
箱送![]() 箱;②通过双方议价,买方能以优惠
箱;②通过双方议价,买方能以优惠![]() 成交的概率为
成交的概率为![]() ,以优惠
,以优惠![]() 成交的概率为
成交的概率为![]() .
.
![]() 甲、乙两单位都要在该厂购买
甲、乙两单位都要在该厂购买![]() 箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
![]() 某单位需要这种零件
某单位需要这种零件![]() 箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
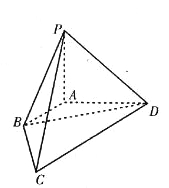
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com