
分析 (1)利用奇函数的定义,求出函数的解析式,即可得出m的值;
(2)分类讨论,可得不等式,解不等式,即可求实数a的取值范围.
解答  解:(1)设x<0,则-x>0,
解:(1)设x<0,则-x>0,
∴f(-x)=-x2-2x,
∵f(x)为奇函数,∴f(-x)=-f(x),
∴f(x)=-f(-x)=x2+2x,
∴m=2;
(2)f(x)在[a,a+$\frac{3}{2}$]上单调递增,∴$\left\{\begin{array}{l}{a≥-1}\\{a+\frac{3}{2}≤1}\end{array}\right.$,∴-1≤a≤-$\frac{1}{2}$;
f(x)在[a,a+$\frac{3}{2}$]上单调递减,∴a+$\frac{3}{2}$≤-1或a≥1,∴a≤$\frac{5}{2}$或a≥1
综上所述,实数a的取值范围是(-∞,-$\frac{5}{2}$]∪[-1,-$\frac{1}{2}$]∪[1,+∞).
点评 本题考查函数的解析式,考查函数的性质,考查函数单调性,考查分类讨论的数学思想,确定函数的解析式是关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1≤x≤0} | C. | {x|1≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
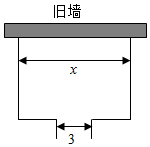 如图所示,要围建一个面积为400m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙时需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为3m的进出口,已知旧墙的维修费用为56元/m,新墙的造价为200元/m,设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元).
如图所示,要围建一个面积为400m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙时需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为3m的进出口,已知旧墙的维修费用为56元/m,新墙的造价为200元/m,设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 偏爱蔬菜 | 偏受肉类 | 合计 | |
| 五十岁以下 | |||
| 五十岁以上 | |||
| 合计 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | 16π | C. | 20π | D. | 32π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com